
分析 根据题意,分析可得要求的圆的圆心是点A(3,8)和B(7,4)的中点,其半径为线段AB长度的一半,分别求出圆心坐标以及半径,即可得答案.
解答 解:根据题意,设A的坐标为(3,8),B的坐标为(7,4)
要求的圆的圆心是点A(3,8)和B(7,4)的中点,
则其圆心的坐标为($\frac{3+7}{2}$,$\frac{8+4}{2}$),即(5,6);
其半径为线段AB长度的一半,即r=$\frac{1}{2}$$\sqrt{(3-7)^{2}+(8-4)^{2}}$=2$\sqrt{2}$,
则要求圆的方程为(x-5)2+(y-6)2=(2$\sqrt{2}$)2,
即(x-5)2+(y-6)2=8,
故答案为:(x-5)2+(y-6)2=8.
点评 本题考查圆的标准方程的求法,求圆的标准方程的关键是找到圆心的坐标以及半径.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
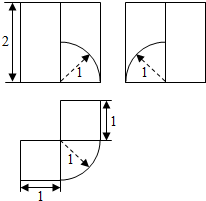
| A. | 6+$\frac{π}{8}$ | B. | 6+$\frac{π}{6}$ | C. | 4+$\frac{π}{8}$ | D. | 4+$\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
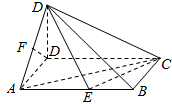 如图,四边形ABCD为矩形,DD1⊥底面ABCD,AD=DD1=$\frac{1}{2}$AB,点F为AD1的中点.点E在棱AB上移动.
如图,四边形ABCD为矩形,DD1⊥底面ABCD,AD=DD1=$\frac{1}{2}$AB,点F为AD1的中点.点E在棱AB上移动.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,F1,F2分别是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a\;,\;b>0)$的左、右两焦点,B是虚轴的端点,直线F1B与C的两条渐近线分别交于P,Q两点,线段PQ的垂直平分线与x轴交于点M.若|MF2|=|F1F2|,则C的离心率是( )
如图,F1,F2分别是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a\;,\;b>0)$的左、右两焦点,B是虚轴的端点,直线F1B与C的两条渐近线分别交于P,Q两点,线段PQ的垂直平分线与x轴交于点M.若|MF2|=|F1F2|,则C的离心率是( )| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com