
【题目】有4位同学在同一天的上午、下午参加“身高与体重”“立定跳远”“肺活量”“握力”“台阶”5个项目的测试,每位同学上午、下午各测试1个项目,且不重复.若上午不测“握力”项目,下午不测“台阶”项目,其余项目上午、下午都各测试1人,则不同的安排方式有多少种?
【答案】264种
【解析】
先分别用甲、乙、丙、丁代表四个同学;用1,2,3,4,5代表这5个项目.根据题意,先确定上午的不同安排方式;再结合题意,不妨设上午的安排是:甲1,乙2,丙3,丁5;讨论:丁下午测试4,丁下午不测试4两种情况,分别求出不同的安排方法,进而可求出结果.
分别用甲、乙、丙、丁代表四个同学;用1,2,3,4,5代表这5个项目.
由条件,上午的安排是1,2,3,5的排列,共有![]() 种;
种;
由于每位同学上午、下午各测试1个项目,且不重复,故下午的安排是1,2,3,4的排列,但不允许出现某同学上午、下午测试同一项目的情况.
不妨设上午的安排是:甲1,乙2,丙3,丁5;
(1)若丁下午测试4,则甲乙丙测试的项目可以为:2,3,1;3,1,2;共2种;
(2)当丁下午不测试4,则丁有![]() 种选择,需从甲乙丙中选择1人测试4,则有
种选择,需从甲乙丙中选择1人测试4,则有![]() 种选择;剩下两人只有1种选择;
种选择;剩下两人只有1种选择;
故下午不同的安排方式有![]() 种;
种;
所以,共有![]() 种不同的安排方式.
种不同的安排方式.


科目:高中数学 来源: 题型:
【题目】对任意实数![]() 给出下列命题:①“
给出下列命题:①“![]() ”是“
”是“![]() ”的充要条件;②“
”的充要条件;②“![]() 是无理数”是“
是无理数”是“![]() 是无理数”的充要条件;③“
是无理数”的充要条件;③“![]() ”是“
”是“![]() ”的充分条件;④“
”的充分条件;④“![]() ”是“
”是“![]() ”的必要条件.其中真命题的个数是( )
”的必要条件.其中真命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司对旗下的甲、乙两个门店在1至9月份的营业额(单位:万元)进行统计并得到如图折线图.

下面关于两个门店营业额的分析中,错误的是( )
A.甲门店的营业额折线图具有较好的对称性,故而营业额的平均值约为32万元
B.根据甲门店的营业额折线图可知,该门店营业额的平均值在[20,25]内
C.根据乙门店的营业额折线图可知,其营业额总体是上升趋势
D.乙门店在这9个月份中的营业额的极差为25万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别是a,b,c,已知sinC+cosC=1-sin![]() .
.
(1)求sinC的值;
(2)若a2+b2=4(a+b)-8,求边c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某课程考核分理论与实验两部分进行,每部分考核成绩只记“合格”与“不合格”,两部分考核都是“合格”,则该课程考核“合格”,若甲、乙、丙三人在理论考核中合格的概率分别为0.9,0.8,0.7,在实验考核中合格的概率分别为0.8,0.7,0.9,所有考核是否合格相互之间没有影响.
(1)求甲、乙、丙三人在理论考核中至少有两人合格的概率;
(2)求这三个人该课程考核都合格的概率(结果保留三位小数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】两城市![]() 和
和![]() 相距
相距![]() ,现计划在两城市外以
,现计划在两城市外以![]() 为直径的半圆
为直径的半圆![]() 上选择一点
上选择一点![]() 建造垃圾处理场,其对城市的影响度与所选地点到城市的距离有关,对城
建造垃圾处理场,其对城市的影响度与所选地点到城市的距离有关,对城![]() 和城
和城![]() 的总影响度为城
的总影响度为城![]() 和城
和城![]() 的影响度之和,记
的影响度之和,记![]() 点到城
点到城![]() 的距离为
的距离为![]() ,建在
,建在![]() 处的垃圾处理场对城
处的垃圾处理场对城![]() 和城
和城![]() 的总影响度为
的总影响度为![]() ,统计调查表明:垃圾处理场对城
,统计调查表明:垃圾处理场对城![]() 的影响度与所选地点到城
的影响度与所选地点到城![]() 的距离的平方成反比,比例系数为4,对城
的距离的平方成反比,比例系数为4,对城![]() 的影响度与所选地点到城
的影响度与所选地点到城![]() 的距离的平方成反比,比例系数为
的距离的平方成反比,比例系数为![]() ,当垃圾处理场建在
,当垃圾处理场建在![]() 的中点时,对城
的中点时,对城![]() 和城
和城![]() 的总影响度为0.065;
的总影响度为0.065;
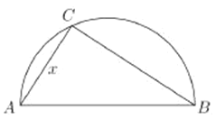
(1)将![]() 表示成
表示成![]() 的函数;
的函数;
(2)判断![]() 上是否存在一点,使建在此处的垃圾处理场对城
上是否存在一点,使建在此处的垃圾处理场对城![]() 和城
和城![]() 的总影响度最小?若存在,求出该点到城
的总影响度最小?若存在,求出该点到城![]() 的距离;若不存在,说明理由;
的距离;若不存在,说明理由;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com