
 ,M(x,y)是f(x)图象上任意一点,其中x=λ
,M(x,y)是f(x)图象上任意一点,其中x=λ +(1-λ)
+(1-λ) ,λ∈[0,1].若不等式|MN|≤k恒成立,则称函数f(x)在[a,b]上满足“k范围线性近似”,其中最小的正实数k称为该函数的线性近似阀值.下列定义在[1,2]上函数中,线性近似阀值最小的是( )
,λ∈[0,1].若不等式|MN|≤k恒成立,则称函数f(x)在[a,b]上满足“k范围线性近似”,其中最小的正实数k称为该函数的线性近似阀值.下列定义在[1,2]上函数中,线性近似阀值最小的是( )


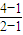 (x-1),即y=3x-2
(x-1),即y=3x-2 )2-
)2- |≤
|≤ ,线性近似阀值为
,线性近似阀值为 .
.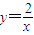 ,由A(1,2),(2,1),AB方程为y=-x+3,|MN|═-x+3-
,由A(1,2),(2,1),AB方程为y=-x+3,|MN|═-x+3-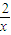 =3-(x+
=3-(x+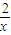 )≤3-2
)≤3-2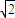 ,线性近似阀值为3-2
,线性近似阀值为3-2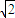 .
.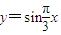 ,A(1,
,A(1,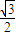 ),B(2,
),B(2,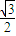 ),AB方程为y=
),AB方程为y=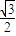 ,由三角函数图象与性质可知|MN|≤1-
,由三角函数图象与性质可知|MN|≤1-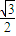 ,线性近似阀值为1-
,线性近似阀值为1-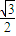 ,
,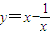 ,得A(1,0),B(2,
,得A(1,0),B(2, ),
), (x-1)
(x-1)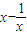 -
- (x-1)=
(x-1)= -(
-(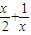 )
)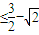 ,线性近似阀值为
,线性近似阀值为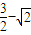 .
. >3-2
>3-2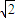 >1-
>1-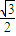 >
> .所以线性近似阀值最小的是
.所以线性近似阀值最小的是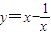


科目:高中数学 来源: 题型:
| ON |
| OA |
| OB |
| MN |
| 1 |
| x |
| A、[0,+∞) | ||||
B、[
| ||||
C、[
| ||||
D、[
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| ON |
| OA |
| OB |
| MN |
| 1 |
| x |
| 3 |
| 2 |
| 2 |
| 3 |
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ON |
| OA |
| OB |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:
. |
| ON |
. |
| OA |
. |
| OB |
| 1 |
| x |
| A、[0,+∞) | ||||||
B、[
| ||||||
C、[
| ||||||
D、[
|
查看答案和解析>>
科目:高中数学 来源:2013年中国人民大学附中高三5月模拟数学试卷(理科)(解析版) 题型:填空题
 ,若不等式
,若不等式 恒成立,则称函数f(x)在[a,b]上“k阶线性近似”.若函数
恒成立,则称函数f(x)在[a,b]上“k阶线性近似”.若函数 在[1,2]上“k阶线性近似”,则实数k的取值范围为 .
在[1,2]上“k阶线性近似”,则实数k的取值范围为 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com