
(12分)经过 作直线
作直线 交曲线
交曲线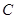 :
: (
(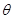 为参数)于
为参数)于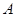 、
、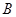 两点,若
两点,若 成等比数列,求直线
成等比数列,求直线 的方程.
的方程.
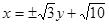
解析试题分析:把曲线的参数方程化为普通方程,由|AB|2=|MA|•|MB|,可得|AB|等于圆的切线长,设出直线l的方程,求出弦心距d,再利用弦长公式求得|AB|,由此求得直线的斜率k的值,即可求得直线l的方程.
解:直线 的参数方程:
的参数方程: (
(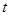 为参数),…………①
为参数),…………①
曲线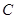 :
: 化为普通方程为
化为普通方程为 ,…………②
,…………②
将①代入②整理得: ,设
,设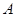 、
、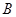 对应的参数分别为
对应的参数分别为 ,
, ,由
,由 成等比数列得:
成等比数列得: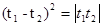 ,
, ,
,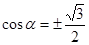 ,
, ,
,
直线 的方程为:
的方程为: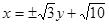
考点:本题主要考查把参数方程化为普通方程的方法,点到直线的距离公式的应用,直线和圆的位置关系,属于基础题.
点评:解决该试题的关键是把曲线的参数方程化为普通方程,由|AB|2=|MA|•|MB|,可得|AB|等于圆的切线长,利用切割线定理得到,并结合勾股定理得到结论。


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com