
【题目】如图所示,将一块直角三角形木板![]() 置于平面直角坐标系中,已知
置于平面直角坐标系中,已知![]() ,点
,点![]() 是三角形木板内一点,现因三角形木板中阴影部分受到损坏,要把损坏部分锯掉,可用经过点
是三角形木板内一点,现因三角形木板中阴影部分受到损坏,要把损坏部分锯掉,可用经过点![]() 的任一直线
的任一直线![]() 将三角形木板锯成
将三角形木板锯成![]() .设直线
.设直线![]() 的斜率为
的斜率为![]() .
.
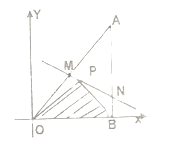
(Ⅰ)求点![]() 的坐标及直线
的坐标及直线![]() 的斜率
的斜率![]() 的范围;
的范围;
(Ⅱ)令![]() 的面积为
的面积为![]() ,试求出
,试求出![]() 的取值范围;
的取值范围;
(Ⅲ)令(Ⅱ)中![]() 的取值范围为集合
的取值范围为集合![]() ,若
,若![]() 对
对![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:
【题目】已知中心在原点,焦点在![]() 轴上的椭圆
轴上的椭圆![]() 过点
过点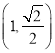 ,离心率为
,离心率为![]() ,
, ![]() ,
, ![]() 是椭圆
是椭圆![]() 的长轴的两个端点(
的长轴的两个端点(![]() 位于
位于![]() 右侧),
右侧),![]() 是椭圆在
是椭圆在![]() 轴正半轴上的顶点.
轴正半轴上的顶点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在经过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() 和
和![]() ,使得向量
,使得向量![]() 与
与![]() 共线?如果存在,求出直线方程;如果不存在,请说明理由.
共线?如果存在,求出直线方程;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人想参加《中国诗词大会》比赛,筹办方要从10首诗司中分别抽出3首让甲、乙背诵,规定至少背出其中2首才算合格; 在这10首诗词中,甲只能背出其中的7首,乙只能背出其中的8首
(1)求抽到甲能背诵的诗词的数量![]() 的分布列及数学期望;
的分布列及数学期望;
(2)求甲、乙两人中至少且有一人能合格的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某企业生产的某种产品中抽取100件,测量这些产品的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间![]() ,
,![]() ,
,![]() 内的频率之比为
内的频率之比为![]() .
.

(Ⅰ)求这些产品质量指标值落在区间![]() 内的频率;
内的频率;
(Ⅱ)用分层抽样的方法在区间![]() 内抽取一个容量为6的样本,将该样本看成一个总体,从中任意
内抽取一个容量为6的样本,将该样本看成一个总体,从中任意
抽取2件产品,求这2件产品都在区间![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设{an}是等差数列,{bn}是各项都为正数的等比数列,且a1=b1=1,a3+b5=21,a5+b3=13.
(1)求{an}、{bn}的通项公式;
(2)求数列 ![]() 的前n项和Sn .
的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆![]() 经过椭圆
经过椭圆![]() 的左右焦点
的左右焦点![]() ,与椭圆
,与椭圆![]() 在第一象限的交点为
在第一象限的交点为![]() ,且
,且![]() ,
, ![]() ,
, ![]() 三点共线.
三点共线.
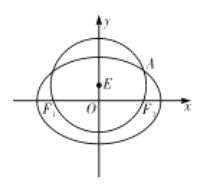
(1)求椭圆![]() 的方程;
的方程;
(2)设与直线![]() (
(![]() 为原点)平行的直线交椭圆
为原点)平行的直线交椭圆![]() 于
于![]() 两点,当
两点,当![]() 的面积取取最大值时,求直线
的面积取取最大值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() 的直角坐标为
的直角坐标为![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于不同的两点
相交于不同的两点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 的三个内角
的三个内角![]() 的对边长分别为
的对边长分别为![]() ,
,![]() 是
是![]() 的外接圆半径,则下列四个条件
的外接圆半径,则下列四个条件
(1)![]() ; (2)
; (2)![]() ;
;
(3)![]() ; (4)
; (4)![]() .
.
有两个结论:甲:![]() 是等边三角形; 乙:
是等边三角形; 乙:![]() 是等腰直角三角形.
是等腰直角三角形.
请你选出给定的四个条件中的两个为条件,两个结论中的一个为结论,写出一个你认为正确的命题__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com