
【题目】某网站从春节期间参与收发网络红包的手机用户中随机抽取![]() 名进行调查,将受访用户按年龄分成
名进行调查,将受访用户按年龄分成![]() 组:
组: ![]() ,
, ![]() ,…,
,…, ![]() ,并整理得到如下频率分布直方图:
,并整理得到如下频率分布直方图:

(Ⅰ)求![]() 的值;
的值;
(Ⅱ)从春节期间参与收发网络红包的手机用户中随机抽取一人,估计其年龄低于![]() 岁的概率;
岁的概率;
(Ⅲ)估计春节期间参与收发网络红包的手机用户的平均年龄.
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:
【题目】已知矩形ABCD的边AB=2,BC=1,以A为坐标原点,AB,AD边分别在x轴、y轴的正半轴上,建立直角坐标系。将矩形折叠,使A点落在线段DC上,重新记为点![]()
(1)当点![]() 坐标为(1,1)时,求折痕所在直线方程.
坐标为(1,1)时,求折痕所在直线方程.
(2)若折痕所在直线的斜率为k,试求折痕所在直线的方程;
(3)当![]() 时,设折痕所在直线与
时,设折痕所在直线与![]() 轴交于点E,与
轴交于点E,与![]() 轴交于点F,将
轴交于点F,将![]() 沿折痕EF旋转.使二面角
沿折痕EF旋转.使二面角![]() 的大小为
的大小为![]() ,设三棱锥
,设三棱锥![]() 的外接球表面积为
的外接球表面积为![]() ,试求
,试求![]() 最小值.
最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=3sin(2x+ ![]() )的图象向右平移
)的图象向右平移 ![]() 个单位长度,所得图象对应的函数( )
个单位长度,所得图象对应的函数( )
A.在区间[ ![]() ,
, ![]() ]上单调递减
]上单调递减
B.在区间[ ![]() ,
, ![]() ]上单调递增
]上单调递增
C.在区间[﹣ ![]() ,
, ![]() ]上单调递减
]上单调递减
D.在区间[﹣ ![]() ,
, ![]() ]上单调递增
]上单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:
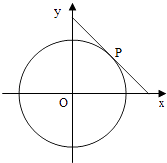
【题目】圆x2+y2=4的切线与x轴正半轴,y轴正半轴围成一个三角形,当该三角形面积最小时,切点为P(如图),双曲线C1: ![]() 过点P且离心率为
过点P且离心率为 ![]() .
. 
(1)求C1的方程;
(2)若椭圆C2过点P且与C1有相同的焦点,直线l过C2的右焦点且与C2交于A,B两点,若以线段AB为直径的圆过点P,求l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三年级共有学生![]() 名,为了解学生某次月考的情况,抽取了部分学生的成绩(得分均为整数,满分为
名,为了解学生某次月考的情况,抽取了部分学生的成绩(得分均为整数,满分为![]() 分)进行统计,绘制出如下尚未完成的频率分布表:
分)进行统计,绘制出如下尚未完成的频率分布表:
分组 | 频数 | 频率 |
|
|
|
|
| |
|
| |
|
| |
| ||
|
|
(1)补充完整题中的频率分布表;
(2)若成绩在![]() 为优秀,估计该校高三年级学生在这次月考中,成绩优秀的学生约为多少人.
为优秀,估计该校高三年级学生在这次月考中,成绩优秀的学生约为多少人.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】教材上一例问题如下:
一只红铃虫的产卵数y和温度x有关,现收集了7组观测数据如下表,试建立y与x之间的回归方程.
温度 x/℃ | 21 | 23 | 25 | 27 | 29 | 32 | 35 |
产卵数y/个 | 7 | 11 | 21 | 24 | 66 | 115 | 325 |
某同学利用图形计算器研究它时,先作出散点图(如图所示),发现两个变量不呈线性相关关系. 根据已有的函数知识,发现样本点分布在某一条指数型曲线![]() 的附近(
的附近(![]() 和
和![]() 是待定的参数),于是进行了如下的计算:
是待定的参数),于是进行了如下的计算:
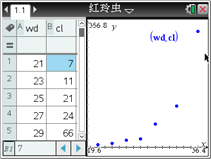
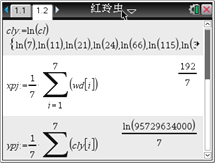
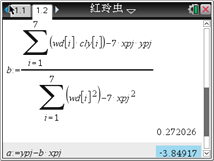
根据以上计算结果,可以得到红铃虫的产卵数y对温度x的回归方程为__________.(精确到0.0001) (提示:![]() 利用代换可转化为线性关系)
利用代换可转化为线性关系)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分16分)甲方是一农场,乙方是一工厂,由于乙方生产须占用甲方的资源,因此甲方每年向乙方索赔以弥补经济损失并获得一定净收入.乙方在不赔付甲方的情况下,乙方的年利润![]() (元)与年产量
(元)与年产量![]() (吨)满足函数关系
(吨)满足函数关系![]() .若乙方每生产一吨产品必须赔付甲方
.若乙方每生产一吨产品必须赔付甲方![]() 元(以下称
元(以下称![]() 为赔付价格).
为赔付价格).
(Ⅰ)将乙方的年利润w (元)表示为年产量![]() (吨)的函数,并求出乙方获得最大利润的年产量;
(吨)的函数,并求出乙方获得最大利润的年产量;
(Ⅱ)甲方每年受乙方生产影响的经济损失金额![]() (元),在乙方按照获得最大利润的产量进行生产的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格
(元),在乙方按照获得最大利润的产量进行生产的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格![]() 是多少?
是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x),g(x)满足 ![]() f(x)g(x)dx=0,则f(x),g(x)为区间[﹣1,1]上的一组正交函数,给出三组函数:
f(x)g(x)dx=0,则f(x),g(x)为区间[﹣1,1]上的一组正交函数,给出三组函数:
①f(x)=sin ![]() x,g(x)=cos
x,g(x)=cos ![]() x;
x;
②f(x)=x+1,g(x)=x﹣1;
③f(x)=x,g(x)=x2 ,
其中为区间[﹣1,1]上的正交函数的组数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com