解:(1)∵
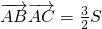
,
∴
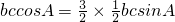
,即
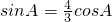
.…(2分)
代入sin
2A+cos
2A=1化简整理,得
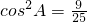
.…(4分)
∵
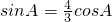
,可得cosA>0,
∴角A是锐角,可得
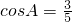
.…(6分)
(2)∵a,b,c成等差数列
∴2b=a+c,结合正弦定理得2sinB=sinA+sinC,
即2sin(A+C)=sinA+sinC,…(8分)
因此,可得2sinAcosC+2cosAsinC=sinA+sinC.①
由(1)得
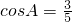
及
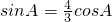
,所以
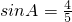
,…(10分)
代入①,整理得
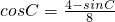
.
结合sin
2C+cos
2C=1进行整理,得65sin
2C-8sinC-48=0,…(12分)
解之得
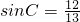
或
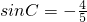
.
∵C∈(0,π),可得sinC>0
∴
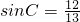
(负值舍去).…(14分)
分析:(1)根据数量积的定义和正弦定理关于面积的公式,化简题中等式可得
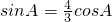
,结合同角三角函数的基本关系可解出cosA的值;
(2)根据等差数列的性质,结合正弦定理化简得2sinB=sinA+sinC,用三角内角和定理进行三角恒等变换得到2sinAcosC+2cosAsinC=sinA+sinC.将(1)中算出的cosA、sinA的值代入,并结合同角三角函数的基本关系,即可求出
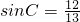
.
点评:本题在三角形ABC中给出
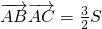
,求角A的余弦,并在已知a,b,c成等差数列情况下求角C的正弦,着重考查了利用正、余弦定理解三角形和三角形的面积公式等知识,属于基础题.

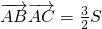 .
.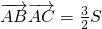 ,
,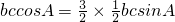 ,即
,即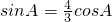 .…(2分)
.…(2分)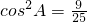 .…(4分)
.…(4分)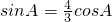 ,可得cosA>0,
,可得cosA>0,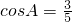 .…(6分)
.…(6分)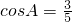 及
及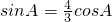 ,所以
,所以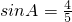 ,…(10分)
,…(10分)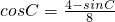 .
.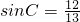 或
或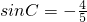 .
.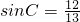 (负值舍去).…(14分)
(负值舍去).…(14分)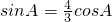 ,结合同角三角函数的基本关系可解出cosA的值;
,结合同角三角函数的基本关系可解出cosA的值;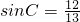 .
.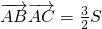 ,求角A的余弦,并在已知a,b,c成等差数列情况下求角C的正弦,着重考查了利用正、余弦定理解三角形和三角形的面积公式等知识,属于基础题.
,求角A的余弦,并在已知a,b,c成等差数列情况下求角C的正弦,着重考查了利用正、余弦定理解三角形和三角形的面积公式等知识,属于基础题. 

 如图,已知△ABC的面积为14,D、E分别为边AB、BC上的点,且AD:DB=BE:EC=2:1,AE与CD交于P.设存在λ和μ使
如图,已知△ABC的面积为14,D、E分别为边AB、BC上的点,且AD:DB=BE:EC=2:1,AE与CD交于P.设存在λ和μ使 (2012•温州一模)如图,在△ABC中,AD⊥BC,垂足为D,且BD:DC:AD=2:3:6.
(2012•温州一模)如图,在△ABC中,AD⊥BC,垂足为D,且BD:DC:AD=2:3:6.