
【题目】函数f(x)=|x|﹣ ![]() (a∈R)的图象不可能是( )
(a∈R)的图象不可能是( )
A.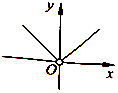
B.
C.
D.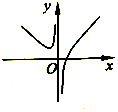
【答案】C
【解析】解:f(x)= 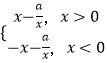 ,∴f′(x)=
,∴f′(x)=  .(1)当a=0时,f(x)=
.(1)当a=0时,f(x)= ![]() ,图象为A;(2)当a>0时,1+
,图象为A;(2)当a>0时,1+ ![]() >0,∴f(x)在(0,+∞)上单调递增,
>0,∴f(x)在(0,+∞)上单调递增,
令﹣1+ ![]() =0得x=﹣
=0得x=﹣ ![]() ,∴当x<﹣
,∴当x<﹣ ![]() 时,﹣1+
时,﹣1+ ![]() <0,当﹣
<0,当﹣ ![]() <x<0时,﹣1+
<x<0时,﹣1+ ![]() >0,
>0,
∴f(x)在(﹣∞,﹣ ![]() )上单调递减,在(﹣
)上单调递减,在(﹣ ![]() ,0)上单调递增,图象为D;(3)当a<0时,﹣1+
,0)上单调递增,图象为D;(3)当a<0时,﹣1+ ![]() <0,∴f(x)在(﹣∞,0)上单调递减,
<0,∴f(x)在(﹣∞,0)上单调递减,
令1+ ![]() =0得x=
=0得x= ![]() ,∴当x>
,∴当x> ![]() 时,1+
时,1+ ![]() >0,当0<x<
>0,当0<x< ![]() 时,1+
时,1+ ![]() <0,
<0,
∴f(x)在(0, ![]() )上单调递减,在(
)上单调递减,在( ![]() ,+∞)上单调递增,图象为B;
,+∞)上单调递增,图象为B;
故选C.
【考点精析】本题主要考查了函数的图象的相关知识点,需要掌握函数的图像是由直角坐标系中的一系列点组成;图像上每一点坐标(x,y)代表了函数的一对对应值,他的横坐标x表示自变量的某个值,纵坐标y表示与它对应的函数值才能正确解答此题.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC﹣A1B1C1中,AC⊥BC,AC=BC= ![]() AA1=1,D是棱AA1上的点,DC1⊥BD
AA1=1,D是棱AA1上的点,DC1⊥BD
(Ⅰ)求证:D为AA1中点;
(Ⅱ)求直线BC1与平面BDC所成角正弦值大小;
(Ⅲ)在△ABC边界及内部是否存在点M,使得B1M⊥面BDC,存在,说明M位置,不存在,说明理由.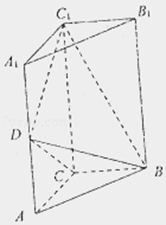
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)为偶函数,当x<0时,f(x)=ln(﹣x)﹣ax.若直线y=x与曲线y=f(x)至少有两个交点,则实数a的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ax(a>0),设 ![]() .
.
(1)判断函数h(x)=f(x)﹣g(x)零点的个数,并给出证明;
(2)首项为m的数列{an}满足:①an+1+an≠ ![]() ;②f(an+1)=g(an).其中0<m<
;②f(an+1)=g(an).其中0<m< ![]() .求证:对于任意的i,j∈N* , 均有ai﹣aj<
.求证:对于任意的i,j∈N* , 均有ai﹣aj< ![]() ﹣m.
﹣m.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某经销商从外地水产养殖厂购进一批小龙虾,并随机抽取40只进行统计,按重量分类统计结果如图: 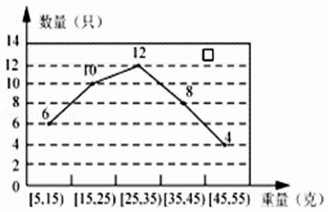
(1)记事件A为:“从这批小龙虾中任取一只,重量不超过35g的小龙虾”,求P(A)的估计值;
(2)若购进这批小龙虾100千克,试估计这批小龙虾的数量;
(3)为适应市场需求,了解这批小龙虾的口感,该经销商将这40只小龙虾分成三个等级,如下表:
等级 | 一等品 | 二等品 | 三等品 |
重量(g) | [5,25) | [25,45) | [45,55] |
按分层抽样抽取10只,再随机抽取3只品尝,记X为抽到二等品的数量,求抽到二级品的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex(x﹣b)(b∈R).若存在x∈[ ![]() ,2],使得f(x)+xf′(x)>0,则实数b的取值范围是( )
,2],使得f(x)+xf′(x)>0,则实数b的取值范围是( )
A.(﹣∞, ![]() )
)
B.(﹣∞, ![]() )
)
C.(﹣ ![]() ,
, ![]() )
)
D.( ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,BC=2AB=4,∠ABC=60°,PA⊥AD,E,F分别为BC,PE的中点,AF⊥平面PED. 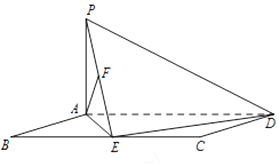
(1)求证:PA⊥平面ABCD
(2)求直线BF与平面AFD所成角的正弦值. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com