
【题目】如图,已知点F为抛物线![]() 的焦点,过点F的动直线l与抛物线C交于M,N两点,且当直线l的倾斜角为
的焦点,过点F的动直线l与抛物线C交于M,N两点,且当直线l的倾斜角为![]() 时,
时,![]() .
.
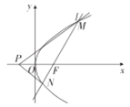
(1)求抛物线C的方程.
(2)点![]() ,证明:直线PM,PN关于x轴对称.
,证明:直线PM,PN关于x轴对称.
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案科目:高中数学 来源: 题型:
【题目】设![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点.
的左、右焦点.
(1)若![]() 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求![]() 的最大值和最小值;
的最大值和最小值;
(2)设过定点![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,且
,且![]() 为锐角(其中
为锐角(其中![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题:
①若将一组样本数据中的每个数据都加上同一个常数后,则样本的方差不变;
②在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高;
③若两个变量间的线性相关关系越强,则相关系数![]() 的值越接近于1;
的值越接近于1;
④对分类变量![]() 与
与![]() 的随机变量
的随机变量![]() 的观测值
的观测值![]() 来说,
来说,![]() 越小,判断“
越小,判断“![]() 与
与![]() 有关系”的把握越大.
有关系”的把握越大.
其中正确的命题序号是( )
A.①②③B.①②C.①③④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:kx-y+1+2k=0(k∈R).
(1)证明:直线l过定点;
(2)若直线不经过第四象限,求k的取值范围;
(3)若直线l交x轴负半轴于A,交y轴正半轴于B,△AOB的面积为S(O为坐标原点),求S的最小值并求此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某民航部门统计的2019年春运期间12个城市售出的往返机票的平均价格以及相比上年同期变化幅度的数据统计图表如图所示,根据图表,下面叙述不正确的是( )
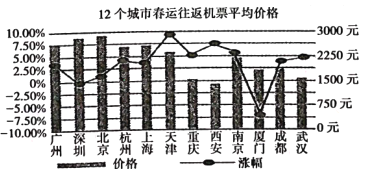
A. 同去年相比,深圳的变化幅度最小且厦门的平均价格有所上升
B. 天津的平均价格同去年相比涨幅最大且2019年北京的平均价格最高
C. 2019年平均价格从高到低居于前三位的城市为北京、深圳、广州
D. 同去年相比,平均价格的涨幅从高到低居于前三位的城市为天津、西安、南京
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() 是椭圆短轴的一个顶点,且
是椭圆短轴的一个顶点,且![]() 是面积为
是面积为![]() 的等腰直角三角形.
的等腰直角三角形.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知直线![]() :
:![]() 与椭圆
与椭圆![]() 交于不同的
交于不同的![]() ,
,![]() 两点,若椭圆
两点,若椭圆![]() 上存在点
上存在点![]() ,使得四边形
,使得四边形![]() 恰好为平行四边形,求直线
恰好为平行四边形,求直线![]() 与坐标轴围成的三角形面积的最小值.
与坐标轴围成的三角形面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市一次全市高中男生身高统计调查数据显示:全市100000名男生的身高服从正态分布N(168,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于160 cm和184 cm之间,将测量结果按如下方式分成6组:第1组[160,164),第2组[164,168),…,第6组[180,184],如图是按上述分组方法得到的频率分布直方图.
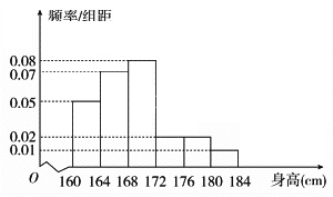
(1)由频率分布直方图估计该校高三年级男生平均身高状况;
(2)求这50名男生身高在172 cm以上(含172 cm)的人数;
(3)在这50名男生身高在172 cm以上(含172 cm)的人中任意抽取2人,将该2人中身高排名(从高到低)在全市前130名的人数记为ξ,求ξ的数学期望.
参考数据:若ξ~N(μ,σ2),则P(μ-σ<ξ≤μ+σ)=0.6826,P(μ-2σ<ξ≤μ+2σ)=0.9544,P(μ-3σ<ξ≤μ+3σ)=0.9974.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在梯形![]() 中(图1),
中(图1),![]() ,
,![]() ,
,![]() ,过
,过![]() 、
、![]() 分别作
分别作![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() 、
、![]() ,且
,且![]() ,将梯形
,将梯形![]() 沿
沿![]() 、
、![]() 同侧折起,使得
同侧折起,使得![]() ,且
,且![]() ,得空间几何体
,得空间几何体![]() (图2).直线
(图2).直线![]() 与平面
与平面![]() 所成角的正切值是
所成角的正切值是![]() .
.
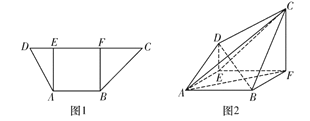
(1)求证:![]() 平面
平面![]() ;
;
(2)求多面体![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com