练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
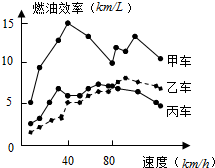
    12．汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程，如图描述了甲、乙、丙三两汽车在不同速度下的燃油效率情况．某城市机动车最高限速80千米/小时，相同条件下，用甲、乙、丙三两汽车在该市行驶，最省油是（　　）
    A．甲车B．乙车C．丙车D．无法确定

    分析 根据汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程，以及图象，即可判断．

    解答 解：由图象可知，甲车的燃油效率最高，故以相同速度行驶相同路程，三辆车中，甲车消耗汽油最小，
    故选：A．

    点评 本题考查了函数图象的识别，关键掌握题意，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    2．已知f（x）=mx（m为常数，m＞0且m≠1）．设$f（{a_1}），f（{a_2}），…，f（{a_n}）（n∈{N^*}）$是首项为4，公比为2的等比数列．
    （1）求数列{an}的通项公式；
    （2）若bn=an•f（an），且数列{bn}的前n项和Sn，当$m=\sqrt{2}$时，求Sn；
    （3）若cn=an•f（n），问是否存在实数m，使得数列{cn}中每一项恒小于它后面的项？若存在，求出实数m的取值范围；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．写出函数y=|x-1|的单调增区间是[1，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．直线l与椭圆$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{3}=1$相交于A、B两点，且线段AB的中点为M（1，1），则直线l的方程为x+3y-4=0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1（a＞b＞0）$的离心率为$\frac{\sqrt{3}}{2}$，右焦点到右准线的距离为$\frac{\sqrt{3}}{3}$．
    （1）求椭圆C的方程
    （2）如图，点M，N为椭圆上相异的两点，其中点M在第一象限，且直线AM与直线BN的斜率互为相反数．
    ①证明：直线MN的斜率为常数
    ②求四边形AMBN面积S的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．设全集U={x|0＜x＜9，x∈N*}，若A∩B={2，3}，A∩∁UB={1，5，7}，∁UA∩∁UB={6}，则集合B={2，3，4，8}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知m为一条直线，α，β为两个不同的平面，则下列说法正确的是（　　）
    A．若m∥α，α∥β，则m∥βB．若α⊥β，m⊥α，则m⊥βC．若m∥α，α⊥β，则m⊥βD．若m⊥α，α∥β，则m⊥β

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．下列函数f（x）与g（x）是相同函数的是（　　）
    A．$f（x）=\sqrt{{{（x-1）}^2}}$；g（x）=x-1B．$f（x）=\frac{{{x^2}-1}}{x-1}$；g（x）=x+1
    C．f（x）=lg（x+1）+lg（x-1）；g（x）=lg（x2-1）D．f（x）=ex+1．ex-1；g（x）=e2x

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知函数$f（x）=cos（{2x-\frac{π}{3}}）+{sin^2}x-{cos^2}x+\sqrt{2}$．
    （1）求函数f（x）的最小正周期和单调递增区间；
    （2）若存在$t∈[{\frac{π}{12}，\frac{π}{3}}]$满足[f（t）]2-2$\sqrt{2}$f（t）-m＞0，求实数m的取值范围．

    查看答案和解析>>

    同步练习册答案