
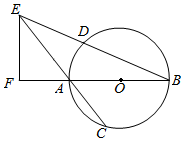
 如图,AB是圆O的直径,弦BD,CA的延长线相交于点E,过E作BA的延长线的垂线,垂足为F.求证:AB2=BE•BD-AE•AC.
如图,AB是圆O的直径,弦BD,CA的延长线相交于点E,过E作BA的延长线的垂线,垂足为F.求证:AB2=BE•BD-AE•AC. 分析 连接AD,利用AB为圆的直径结合EF与AB的垂直关系,通过证明A,D,E,F四点共圆知,BD•BE=BA•BF,再利用△ABC∽△AEF得到比例式,最后利用线段间的关系即求得AB2=BE•BD-AE•AC.
解答 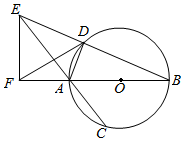 证明:连接AD,因为AB为圆的直径
证明:连接AD,因为AB为圆的直径
所以∠ADB=90°,
又EF⊥AB,∠AFE=90°,
则A,D,E,F四点共圆,
∴BD•BE=BA•BF,
又△ABC∽△AEF,
∴$\frac{AB}{AE}=\frac{AC}{AF}$,即AB•AF=AE•AC
∴BE•BD-AE•AC=BA•BF-AB•AF=AB•(BF-AF)=AB2.
点评 本小题主要考查与圆有关的比例线段、四点共圆的证明方法、三角形相似等基础知识,考查运算求解能力、化归与转化思想.属于中档题.


科目:高中数学 来源: 题型:解答题
 如图,矩形ABCD所在的平面和平面ABEF互相垂直,等腰梯形ABEF中,AB∥EF,AB=2AF=2AD,∠BAF=60°.
如图,矩形ABCD所在的平面和平面ABEF互相垂直,等腰梯形ABEF中,AB∥EF,AB=2AF=2AD,∠BAF=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{7}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com