已知函数f(x)=x|x-a|+2x.
(1)若a=4时,求函数f(x)的单调减区间;
(2)求所有的实数a,使得对任意x∈[1,2]时,函数f(x)的图象恒在函数g(x)=2x+1图象的下方;
(3)若存在a∈[-4,4],使得关于x的方程f(x)=tf(a)有三个不相等的实数根,求实数t的取值范围.
解:(1)a=4时,f(x)=x|x-4|+2x=

,
当x≥4时,f(x)=x
2-2x的增区间是[4,+∞),无减区间.
当x<4时,f(x)=6x-x
2增区间是(-∞,3],减区间是[3,4],
综上所述,f(x)的单调减区间为[3,4].…(4分)
(2)由题意得对任意的实数x∈[1,2],f(x)<g(x)恒成立,
即x|x-a|<1,当x∈[1,2]恒成立,即|x-a|<

,-

,
x-

,故只要x-

<a,且a<x+

在x∈[1,2]上恒成立即可,
在x∈[1,2]时,只要x-

的最大值小于a,
且x+

的最小值大于a即可,…(6分)
而当x∈[1,2]时,(1-

)′=1+

>0,x-

为增函数,

;
当x∈[1,2]时,(x+

)′=1-

>0,x+

为增函数,(x+

)
min=2,
所以

.…(10分)
(3)当-2≤a≤2时,f(x)在R上是增函数,
则关于x的方程f(x)=tf(a)不可能有三个不等的实数根,…(11分)
则当a∈(2,4]时,由f(x)=

,
得x≥a时,f(x)=x
2+(2-a)x,对称轴x=

,
则f(x)在x∈[a,+∞)为增函数,此时f(x)的值域为[f(a),+∞)=[2a,+∞),
x<a时,f(x)=-x
2+(2+a)x,对称轴x=

,
则f(x)在x∈(-∞,
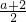
]为增函数,此时f(x)的值域为(-∞,

],
f(x)在x∈[
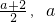
)为减函数,此时f(x)的值域为(2a,

];
由存在a∈(2,4],方程f(x)=tf(a)=2ta有三个不相等的实根,
则2ta∈(2a,

),
即存在a∈(2,4],使得t∈(1,

)即可,
令g(a)=

=
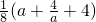
,
只要使t<(g(a))
max即可,而g(a)在a∈(2,4]上是增函数,
∴

,
故实数t的取值范围为(1,

);…(15分)
同理可求当a∈[-4,-2)时,t的取值范围为(1,

);
综上所述,实数t的取值范围为(1,

).…(17分)
分析:(1)a=4时,f(x)=

,由此能求出f(x)的单调减区间.
(2)由题意得对任意的实数x∈[1,2],f(x)<g(x)恒成立,即x|x-a|<1,当x∈[1,2]恒成立,由此能求出所有的实数a.
(3)当-2≤a≤2时,f(x)在R上是增函数,则关于x的方程f(x)=tf(a)不可能有三个不等的实数根;当a∈(2,4]时和当a∈[-4,-2)时,等价转化f(x)的表达式,利用函数的单调性能得到实数t的取值范围.
点评:本题考查函数恒成立问题的应用,考查运算求解能力,推理论证能力;考查化归与转化思想.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.

 ,
, ,-
,- ,
, ,故只要x-
,故只要x- <a,且a<x+
<a,且a<x+ 在x∈[1,2]上恒成立即可,
在x∈[1,2]上恒成立即可, 的最大值小于a,
的最大值小于a, 的最小值大于a即可,…(6分)
的最小值大于a即可,…(6分) )′=1+
)′=1+ >0,x-
>0,x- 为增函数,
为增函数, ;
; )′=1-
)′=1- >0,x+
>0,x+ 为增函数,(x+
为增函数,(x+ )min=2,
)min=2, .…(10分)
.…(10分) ,
, ,
, ,
,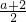 ]为增函数,此时f(x)的值域为(-∞,
]为增函数,此时f(x)的值域为(-∞, ],
],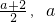 )为减函数,此时f(x)的值域为(2a,
)为减函数,此时f(x)的值域为(2a, ];
]; ),
), )即可,
)即可, =
=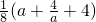 ,
, ,
, );…(15分)
);…(15分) );
); ).…(17分)
).…(17分) ,由此能求出f(x)的单调减区间.
,由此能求出f(x)的单调减区间.

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<