
【题目】古希腊人常用小石子在沙滩上摆成各种形状来研究数,例如:

他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似地,称图2中的1,4,9,16,…这样的数为正方形数.下列数中既是三角形数又是正方形数的是
A. 289 B. 1 024 C. 1 225 D. 1 378
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,椭圆C: ![]() =1(a>1)的左、右顶点分别为A、B,P是椭圆C上任一点,且点P位于第一象限.直线PA交y轴于点Q,直线PB交y轴于点R.当点Q坐标为(0,1)时,点R坐标为(0,2)
=1(a>1)的左、右顶点分别为A、B,P是椭圆C上任一点,且点P位于第一象限.直线PA交y轴于点Q,直线PB交y轴于点R.当点Q坐标为(0,1)时,点R坐标为(0,2) 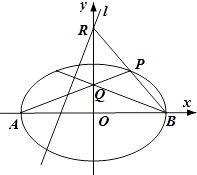
(1)求椭圆C的标准方程;
(2)求证: ![]() 为定值;
为定值;
(3)求证:过点R且与直线QB垂直的直线经过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知M,N是焦点为F的抛物线y2=2px(p>0)上两个不同的点,线段MN的中点A的横坐标为![]() .
.
(1)求|MF|+|NF|的值;
(2)若p=2,直线MN与x轴交于点B,求点B的横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个特定时段内,以点![]() 为中心的
为中心的![]() 海里以内海域被设为警戒水域.点
海里以内海域被设为警戒水域.点![]() 正北50海里处有一个雷达观测站
正北50海里处有一个雷达观测站![]() .某时刻测得一艘匀速直线行驶的船只位于点
.某时刻测得一艘匀速直线行驶的船只位于点![]() 北偏东
北偏东![]() 且与点
且与点![]() 相距
相距![]() 海里的位置
海里的位置![]() ,经过
,经过![]() 分钟又测得该船已行驶到点
分钟又测得该船已行驶到点![]() 北偏东
北偏东![]() 且与点
且与点![]() 相距
相距![]() 海里的位置
海里的位置![]() .
.
(1)求该船的行驶速度(单位:海里/小时);
(2)若该船不改变航行方向继续行驶,判断它是否会进入警戒水域,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},{bn}均为各项都不相等的数列,Sn为{an}的前n项和,an+1bn=Sn+1(n∈N).
(1)若a1=1,bn= ![]() ,求a4的值;
,求a4的值;
(2)若{an}是公比为q的等比数列,求证:存在实数λ,使得{bn+λ}为等比数列;
(3)若{an}的各项都不为零,{bn}是公差为d的等差数列,求证:a2 , a3 , …,an…成等差数列的充要条件是d= ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() (其中a>0,且a≠1).
(其中a>0,且a≠1).
(1)请你推测g(5)能否用f(2),f(3),g(2),g(3)来表示;
(2)如果(1)中获得了一个结论,请你推测能否将其推广.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为评估设备![]() 生产某种零件的性能,从设备
生产某种零件的性能,从设备![]() 生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
直径mm | 58 | 59 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 73 | 合计 |
件数 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
经计算,样本的平均值![]() ,标准差
,标准差![]() ,以频率值作为概率的估计值.
,以频率值作为概率的估计值.
(1)为评判一台设备的性能,从该设备加工的零件中任意抽取一件,记其直径为![]() ,并根据以下不等式进
,并根据以下不等式进
行评判(![]() 表示相应事件的概率);①
表示相应事件的概率);①![]() ;②
;②![]() ;③
;③![]() .
.
评判规则为:若同时满足上述三个不等式,则设备等级为甲;仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部不满足,则等级为丁,试判断设备![]() 的性能等级.
的性能等级.
(2)将直径小于等于![]() 或直径大于
或直径大于![]() 的零件认为是次品.
的零件认为是次品.
(ⅰ)从设备![]() 的生产流水线上随意抽取2件零件,计算其中次品个数
的生产流水线上随意抽取2件零件,计算其中次品个数![]() 的数学期望
的数学期望![]() ;
;
(ⅱ)从样本中随意抽取2件零件,计算其中次品个数![]() 的数学期望
的数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆 ![]() =1(a>b>0)的左、右顶点分别为A,B,焦距为2
=1(a>b>0)的左、右顶点分别为A,B,焦距为2 ![]() ,直线x=﹣a与y=b交于点D,且|BD|=3
,直线x=﹣a与y=b交于点D,且|BD|=3 ![]() ,过点B作直线l交直线x=﹣a于点M,交椭圆于另一点P.
,过点B作直线l交直线x=﹣a于点M,交椭圆于另一点P. 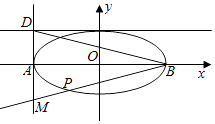
(1)求椭圆的方程;
(2)证明: ![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com