
【题目】某校从参加高一年级期末考试的学生中抽出40名学生,将其成绩分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图,观察图形的信息,回答下列问题:
(1)求第四小组的频率![]() ;
;
(2)估计这次考试的平均分和中位数(精确到0.01);
(3)从成绩是40~50分及90~100分的学生中选两人,记他们的成绩分别为![]() ,求满足“
,求满足“![]() ”的概率.
”的概率.
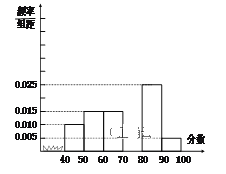
【答案】(1)0.3(2)平均分71,中位数73.33(3)![]()
【解析】
(1)由频率分布直方图直接求出第4小组的频率.
(2)由频率分布直方图能估计平均分和中位数.
(3)设成绩满足“|x﹣y|≤10”为事件A,由频率分布直方图得成绩在[40,50)分的学生记为1,2,3,4,成绩在[90,100)分的学生记为a,b,将从成绩是40~50分及90~100分的学生中选两人的基本事件一一列出,从中找出事件A包含的基本事件,由此能求出满足“|x﹣y|≤10”的概率.
(1)由频率分布直方图可知
所以第4小组的频率为:a=1﹣0.1﹣0.15﹣0.15﹣0.25﹣0.05=0.3.
(2)由频率分布直方图可得平均分为:
0.1×45+0.15×55+0.15×65+0.3×75+0.25×85+0.05×95=71
第一、二、三组的频率之和为0.1+0.15+0.15=0.4
所以中位数= 70+![]() ≈73.33
≈73.33
(3)由频率分布直方图可得,成绩是40~50分的有40×0.1=4人,记为1,2,3,4,90~100分的学生有40×0.05=2人,记为a,b.
记“|x﹣y| ≤10”为事件A,
基本事件有(1,2) (1,3) (1,4) (1,a) (1,b) (2,3) (2,4) (2,a) (2,b) (3,4) (3,a) (3,b) (4,a) (4,b) (a,b) 共计15个, 事件A中包含的基本事件数为(1,2) (1,3) (1,4) (2,3) (2,4) (3,4) (a,b)共7个.
所以 P(A)=![]() .
.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 的部分图象如图所示,则下列判断错误的是( )
的部分图象如图所示,则下列判断错误的是( )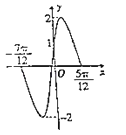
A.ω=2
B.![]()
C.函数f(x)的图象关于(﹣![]() , 0)对称
, 0)对称
D.函数f(x)的图象向右平移![]() 个单位后得到y=Asinωx的图象
个单位后得到y=Asinωx的图象
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)=log2( ![]() +a).
+a).
(1)当a=5时,解不等式f(x)>0;
(2)若关于x的方程f(x)﹣log2[(a﹣4)x+2a﹣5]=0的解集中恰好有一个元素,求a的取值范围.
(3)设a>0,若对任意t∈[ ![]() ,1],函数f(x)在区间[t,t+1]上的最大值与最小值的差不超过1,求a的取值范围.
,1],函数f(x)在区间[t,t+1]上的最大值与最小值的差不超过1,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正数a、b、c成等比数列,则下列三数也成等比数列的是( )
A.lga , lgb , lgc
B.10a , 10b , 10c
C.5lga5lgb5lgc
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足an = nkn(n∈N* , 0 < k < 1),下面说法正确的是( )
①当 ![]() 时,数列{an}为递减数列;
时,数列{an}为递减数列;
②当 ![]() 时,数列{an}不一定有最大项;
时,数列{an}不一定有最大项;
③当 ![]() 时,数列{an}为递减数列;
时,数列{an}为递减数列;
④当 ![]() 为正整数时,数列{an}必有两项相等的最大项.
为正整数时,数列{an}必有两项相等的最大项.
A.①②
B.②④
C.③④
D.②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,若存在x0 , 使得
,若存在x0 , 使得 ![]() ,则x0称是函数
,则x0称是函数 ![]() 的一个不动点,设
的一个不动点,设 ![]()
(1)求函数 ![]() 的不动点;
的不动点;
(2)对(1)中的二个不动点a、b(假设a>b),求使 ![]() 恒成立的常数k的值;
恒成立的常数k的值;
(3)对由a1=1,an= ![]() 定义的数列{an},求其通项公式an .
定义的数列{an},求其通项公式an .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】叙利亚内战接近尾声,中国红十字会相应国际号召,支持叙利亚人民战后重建,为解决现阶段叙利亚人民急需的医疗保障,现拟从北京某知名医院的专职教授的医生6人(其中男医生3人,女医生3人),护士8人(其中男护士2人,女护士6人)中选派医生、护士各三人组成卫生医疗对,要求男医生至少两人,男护士至少一人,则这样的选派方案共有__________种.(请用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题p:在△ABC中,∠C>∠B是sinC>sinB的充分必要条件;命题q:a>b是ac2>bc2的充分不必要条件( )
A.p真q假
B.p假q真
C.“p或q”为假
D.“p且q”为真
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正三棱柱ABC﹣A1B1C1中,已知D,E分别为BC,B1C1的中点,点F在棱CC1上,且EF⊥C1D.求证: 
(1)直线A1E∥平面ADC1;
(2)直线EF⊥平面ADC1 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com