练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在△ABC所在的平面内，点P0、P满足 = ， ，且对于任意实数λ，恒有 ，则（ ）
    A.∠ABC=90°
    B.∠BAC=90°
    C.AC=BC
    D.AB=AC

    【答案】C
    【解析】解：∵ = ， ，∴P0、P、A、B 四点共线，
    以AB所在的直线为x轴，以AB的中垂线为y轴，建立直角坐标系，设AB=4，C（a，b），P（x，0），
    则A（﹣2，0），B（2，0），P0（1，0），
    ∵恒有 ，∴（2﹣x，0）（a﹣x，b）≥（1，0）（a﹣1，b）恒成立，
    即（2﹣x）（a﹣x）≥a﹣1恒成立，
    即 x2﹣（a+2）x+a+1≥0 恒成立，∴判别式△=（a+2）2﹣4（a+1）≤0，
    解得a2≤0，∴a=0，即点C在AB的垂直平分线上，∴CA=CB，
    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，角A，B，C所对的边分别为a，b，c，且cos2 ﹣sinBsinC= ．
    （1）求A；
    （2）若a=4，求△ABC面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题共13分）

    以下茎叶图记录了甲、乙两组各四名同学的植树棵数。乙组记录中有一个数据模糊，无法确认，在图中经X表示。

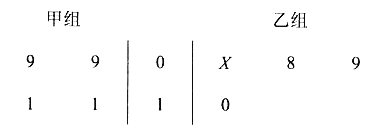
    （Ⅰ）如果X=8，求乙组同学植树棵数的平均数和方差；

    （Ⅱ）如果X=9，分别从甲、乙两组中随机选取一名同学，求这两名同学的植树总棵数为19的概率。

    （注：方差其中为，，的平均数）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列命题中所有正确命题的序号为______．

    若方程表示圆，那么实数；

    已知函数的图象与函数的图象关于直线对称，令，则的图象关于原点对称；

    在正方体中，E、F分别是AB和的中点，则直线CE、F、DA三线共点；

    幂函数的图象不可能经过第四象限．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数.

    （1）求函数的最小正周期；

    （2）求函数的单调递增区间及对称中心；

    （3）函数可以由经过怎样的变换得到.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知与曲线相切的直线，与轴， 轴交于两点， 为原点， ， ，（ ）.

    （1）求证:： 与相切的条件是： .

    （2）求线段中点的轨迹方程；

    （3）求三角形面积的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】把函数f（x）= 图象上各点向右平移（＞0）个单位，得到函数g（x）=sin2x的图象，则的最小值为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了解某冷饮店的经营状况，随机记录了该店月的月营业额（单位：万元）与月份的数据，如下表：

    （1）求关于的回归直线方程；

    （2）若在这些样本点中任取两点，求恰有一点在回归直线上的概率.

    附：回归直线方程中，

    ，.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】Sn为数列{an}的前n项和，已知an＞0，an2+2an=4Sn+3
    （I）求{an}的通项公式；
    （Ⅱ）设bn= ，求数列{bn}的前n项和．

    查看答案和解析>>

    同步练习册答案