练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】有一批材料可以建成80m的围墙，若用此材料在一边靠墙的地方围成一块矩形场地，中间用同样的材料隔成三个面积相等的小矩形（如图所示），且围墙厚度不计，则围成的矩形的最大面积为（ ）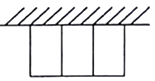
    A.200m2
    B.360m2
    C.400m2
    D.480m2

    【答案】C
    【解析】解：设每个小矩形长为x，宽为y， 则有4x+3y=80，（0＜x＜20）
    围成的矩形的面积S=3xy= ≤ [ ]2=400，当且仅当4x=3y=40时，等号成立，
    即围成的矩形的最大面积为400m2 ，
    故选：C．
    【考点精析】本题主要考查了基本不等式在最值问题中的应用的相关知识点，需要掌握用基本不等式求最值时（积定和最小，和定积最大），要注意满足三个条件“一正、二定、三相等”才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知集合A=[a﹣3，a]，函数 （﹣2≤x≤5）的单调减区间为集合B．
    （1）若a=0，求（RA）∪（RB）；
    （2）若A∩B=A，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）判断的单调性；

    （2）求函数的零点的个数；

    （3）令，若函数在（0，）内有极值，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，已知长方体ABCD﹣A1B1C1D1中，AB=BC=2，AA1=4，E是棱CC1上的点，且BE⊥B1C．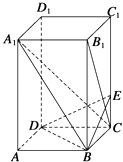

    （1）求CE的长；
    （2）求证：A1C⊥平面BED；
    （3）求A1B与平面BDE夹角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数， ．

    （1）设．

    ①若函数在处的切线过点，求的值；

    ②当时，若函数在上没有零点，求的取值范围；

    （2）设函数，且（），求证：当时， ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】以下命题中，正确命题的序号是 ． ①函数y=tanx在定义域内是增函数；
    ②函数y=2sin（2x+ ）的图象关于x= 成轴对称；
    ③已知 =（3，4）， =﹣2，则向量 在向量 的方向上的投影是﹣
    ④如果函数f（x）=ax2﹣2x﹣3在区间（﹣∞，4）上是单调递减的，则实数a的取值范围是（0， ]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】现有一块大型的广告宣传版面，其形状如图所示的直角梯形．某厂家因产品宣传的需要，拟出资规划出一块区域（图中阴影部分）为产品做广告，形状为直角梯形（点在曲线段上，点在线段上）．已知，，其中曲线段是以为顶点，为对称轴的抛物线的一部分．

    （1）求线段，线段，曲线段所围成区域的面积；

    （2）求厂家广告区域的最大面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为得到函数 的图象，只需将函数y=sin2x的图象（ ）
    A.向左平移 个长度单位
    B.向右平移 个长度单位
    C.向左平移 个长度单位
    D.向右平移 个长度单位

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若函数fA（x）的定义域为A=[a，b），且fA（x）=（ + ﹣1）2﹣ +1，其中a，b为任意正实数，且a＜b．
    （1）求函数fA（x）的最小值和最大值；
    （2）若x1∈Ik=[k2 ， （k+1）2），x2∈Ik+1=[（k+1）2 ， （k+2）2），其中k是正整数，对一切正整数k，不等式 （x1）+ （x2））＜m都有解，求m的取值范围；
    （3）若对任意x1 ， x2 ， x3∈A，都有 ， ， 为三边长构成三角形，求 的取值范围．

    查看答案和解析>>

    同步练习册答案