
 请考生在第22,23,24题中任选一题作答,如果多做,则按所做的第一题记分.作答时请写清题号.
请考生在第22,23,24题中任选一题作答,如果多做,则按所做的第一题记分.作答时请写清题号.| 3 |
| 2 |
| 9 |
| 2 |
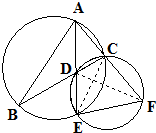 (Ⅰ)证明:如图,连接CE,DF,
(Ⅰ)证明:如图,连接CE,DF,| EF |
| ED |
| AE |
| EF |
| 3 |
| 2 |
| 9 |
| 2 |
| 9 |
| 2 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2011届河南省焦作市高三年级下学期第一次质检数学理卷 题型:解答题
(请考生在第22、23两题中任选一题作 答,如果多做。则按所做的第一题记分.
答,如果多做。则按所做的第一题记分.
(本小题满分10分)选修4-1:几何证明选讲
如图:AB是⊙O的直径,G是AB延长线上的一点,GCD是⊙O的割线,过点G作AG的垂线,交直线AC于点E,交直线AD于点F,过点G作⊙O的切线,切点为H.求证:
(Ⅰ)C、D、F、E四点共圆;
(Ⅱ)GH2=GE·GF.
查看答案和解析>>
科目:高中数学 来源:2010年海南省高三五校联考数学(文) 题型:选择题
选做题:请考生在第22,23,24题中任选一题做答,如果多做,则按所做的第一题记分
22.(本小题满分10分)选修4—1几何证明选讲
如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F。
(I)求证:DE是⊙O的切线;
(II)若 的值.
的值.

23.(本小题满分10分)选修4—2坐标系与参数方程
设直角坐标系原点与极坐标极点重合, x轴正半轴与极轴重合,若已知曲线C的极坐标方程为 ,点F1、F2为其左、右焦点,直线l的参数方程为
,点F1、F2为其左、右焦点,直线l的参数方程为
(I)求直线l的普通方程和曲线C的直角坐标方程;
(II)求曲线C上的动点P到直线l的最大距离。
24.(本小题满分10分)选修4—5不等式选讲
对于任意的实数 恒成立,记实数M的最大值是m。
恒成立,记实数M的最大值是m。
(1)求m的值;
(2)解不等式
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com