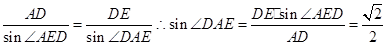试题分析:先通过平移将两条异面直线平移到同一个起点A,得到的锐角或直角就是异面直线所成的角,在三角形中再利用正弦定理求出此角即可.由题意,正方形和菱形变成均为1,又平面ABCD⊥平面CEFB,所以CE⊥平面ABCD,于是CE⊥CD,从而DE=
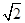
在△ADE中,AD=1,DE=
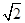
,∠AED=30°,由正弦定理可知
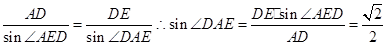
故∠DAE=45°,又BC∥AD,故异面直线BC与AE所成角等于∠DAE,故答案为:45°
点评:直线a,b是异面直线,经过空间一点O,分别引直线A∥a,B∥b,相交直线A,B所成的锐角(或直角)叫做异面直线a,b所成的角.求两条异面直线所成角的大小一般方法是通过平行移动直线,把异面问题转化为共面问题来解决



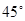
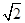
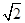 ,∠AED=30°,由正弦定理可知
,∠AED=30°,由正弦定理可知