选修4-5:不等式选讲
设函数f(x)=|x-1|+|x-a|(a∈R)
(1)当a=4时,求不等式f(x)≥5的解集;
(2)若f(x)≥4对x∈R恒成立,求a的取值范围.
解:(Ⅰ)当a=4时,不等式f(x)≥5,即|x-1|+|x-4|≥5,等价于
,
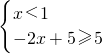
,或
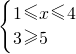
,或
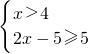
.
解得:x≤0或 x≥5.
故不等式f(x)≥5的解集为 {x|x≤0,或 x≥5 }. …(5分)
(Ⅱ)因为f(x)=|x-1|+|x-a|≥|(x-1)-(x-a)|=|a-1|.(当x=1时等号成立)
所以:f(x)
min=|a-1|.…(8分)
由题意得:|a-1|≥4,解得 a≤-3,或a≥5. …(10分)
分析:(Ⅰ)不等式即|x-1|+|x-4|≥5,等价于
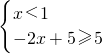
,或
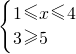
,或
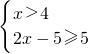
,分别求出每个不等式组的解集,再取并集即得所求.
(Ⅱ)因为f(x)=|x-1|+|x-a|≥|a-1|,由题意可得|a-1|≥4,与偶此解得 a的值.
点评:本题主要考查绝对值不等式的解法,函数的恒成立问题,属于中档题.

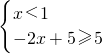 ,或
,或 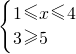 ,或
,或 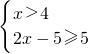 .
.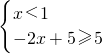 ,或
,或 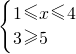 ,或
,或 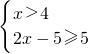 ,分别求出每个不等式组的解集,再取并集即得所求.
,分别求出每个不等式组的解集,再取并集即得所求.
