
设函数 .
.
(Ⅰ)若 时函数
时函数 有三个互不相同的零点,求
有三个互不相同的零点,求 的取值范围;
的取值范围;
(Ⅱ)若函数 在
在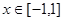 内没有极值点,求
内没有极值点,求 的取值范围;
的取值范围;
(Ⅲ)若对任意的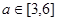 ,不等式
,不等式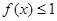 在
在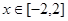 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.
19.(1)当a=1时,f(x)=x3+x2-x+m
f’(x)=3x2+2x-1
令f’(x)=0
则x1=-1或x2=
x (-∞,
-1) -1 (-1, )
)
 (
( ,
+∞)
,
+∞)
f’(x) + 0 - 0 +
f(x) ↑ 极大值 ↓ 极小值 ↑
∴y极大值=f(-1)=-1+1+1+m=m+1
y极小值=f(
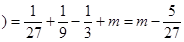

(2) f’(x)=3x2+2ax-a2
依题意:3x2+2ax-a2=0
在[-1, 1]上无实根

(3)f’(x) =(x+a)·(3x-a) (a>0)
x (-∞,
-a) -a (-a,  )
)
 (
( ,+∞)
,+∞)
f’(x) + 0 - 0 +
f(x) ↑ 极大值 ↓ 极小值 ↑
a∈[3, 6]
 ∈[1, 2], -a∈[-6, -3]
∈[1, 2], -a∈[-6, -3]
x (-2,  )
(
)
( ,
2]
,
2]
f’(x) - +
f(x) ↓ ↑
∴f(x)max=max{f(-2), f(2)}
f(-2)=-8+4a+2a2+m
f(2)=8+4a-2a2+m
f(2)-f(-2)=16-4a2<0
∴f(x)max=f(-2)=2a2+4a-8+m
依题意: f(x)max≤1
∴m≤-2a2-4a+9
当a=6时
m≤-87 4‘
【解析】略


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:
(本小题满分13分) 设函数![]() .
.
(1)若![]() 时函数
时函数![]() 有三个互不相同的零点,求
有三个互不相同的零点,求![]() 的取值范围;
的取值范围;
(2)若函数![]() 在
在![]() 内没有极值点,求
内没有极值点,求![]() 的取值范围;
的取值范围;
(3)若对任意的![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数![]() .
.
(1)若![]() 时函数
时函数![]() 有三个互不相同的零点,求
有三个互不相同的零点,求![]() 的取值范围;
的取值范围;
(2)若函数![]() 在
在![]() 内没有极值点,求
内没有极值点,求![]() 的取值范围;
的取值范围;
(3)若对任意的![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江西省高三第二次联考数学文卷 题型:解答题
设函数 。
。
(1)若 时,函数
时,函数 取得极值,求函数
取得极值,求函数 的图像在
的图像在 处的切线方程;
处的切线方程;
(2)若函数 在区间
在区间 内不单调,求实数
内不单调,求实数 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
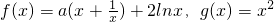 .
. 时,直线l与函数f(x)和函数g(x)的图象相切于同一点,求切线l的方程;
时,直线l与函数f(x)和函数g(x)的图象相切于同一点,求切线l的方程;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com