
分析 把原函数式变形,然后令t=${2}^{x}-{2}^{-x}={2}^{x}-\frac{1}{{2}^{x}}$换元,由x的范围利用单调性求出t的范围,再由配方法求得函数的值域.
解答 解:f(x)=4x+4-x-2x+2-x-4=(2x-2-x)2-(2x-2-x)-2,
令t=${2}^{x}-{2}^{-x}={2}^{x}-\frac{1}{{2}^{x}}$,
∵x∈[0,1),∴t∈[0,$\frac{3}{2}$),
原函数化为g(t)=t2-t-2=$(t-\frac{1}{2})^{2}-\frac{9}{4}$,
当t=$\frac{1}{2}$时,函数有最小值为$-\frac{9}{4}$;
当t=$\frac{3}{2}$时,g(t)=$-\frac{5}{4}$.
∴函数f(x)=4x+4-x-2x+2-x-4,x∈[0,1)的值域为[$-\frac{9}{4},-\frac{5}{4}$).
点评 本题考查函数值域的求法,考查了换元法和配方法求函数的值域,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
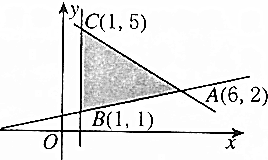 给出平面可行域(如图),若使目标函数z=ax+y取最大值的最优解有无穷多个,则a=( )
给出平面可行域(如图),若使目标函数z=ax+y取最大值的最优解有无穷多个,则a=( )| A. | $\frac{1}{4}$ | B. | $\frac{3}{5}$ | C. | 4 | D. | $\frac{5}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com