
【题目】设a为正实数.如图,一个水轮的半径为a m,水轮圆心 O 距离水面![]() ,已知水轮每分钟逆时针转动 5 圈.当水轮上的点 P 从水中浮现时(即图中点
,已知水轮每分钟逆时针转动 5 圈.当水轮上的点 P 从水中浮现时(即图中点![]() )开始计算时间.
)开始计算时间.

(1)将点 P 距离水面的高度 h(m )表示为时间 t(s)的函数;
(2)点 P 第一次达到最高点需要多少时间.
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,其离心率
,其离心率![]() ,点P为椭圆上的一个动点,
,点P为椭圆上的一个动点,![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆的标准方程;
(2)若A,B,C,D是椭圆上不重合的四个点,AC与BD相交于点![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,PA⊥AC,PA⊥AB,PA=AB,![]() ,
,![]() ,点D,E分别在棱PB,PC上,且DE∥BC,
,点D,E分别在棱PB,PC上,且DE∥BC,
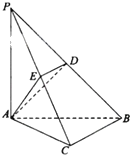
(1)求证:BC⊥平面PAC;
(2)当D为PB的中点时,求AD与平面PAC所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:克)中,经统计得频率分布直方图如图所示.
(单位:克)中,经统计得频率分布直方图如图所示.
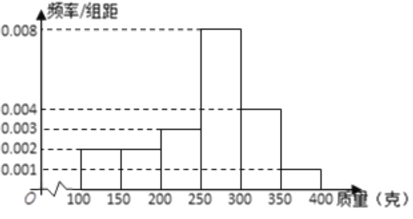
(1) 经计算估计这组数据的中位数;
(2)现按分层抽样从质量为![]() ,
,![]() 的芒果中随机抽取
的芒果中随机抽取![]() 个,再从这
个,再从这![]() 个中随机抽取
个中随机抽取![]() 个,求这
个,求这![]() 个芒果中恰有
个芒果中恰有![]() 个在
个在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1为某省2018年1~4月快递业务量统计图,图2是该省2018年1~4月快递业务收入统计图,下列对统计图理解错误的是( )


A. 2018年1~4月的业务量,3月最高,2月最低,差值接近2000万件
B. 2018年1~4月的业务量同比增长率均超过50%,在3月底最高
C. 从两图来看,2018年1~4月中的同一个月的快递业务量与收入的同比增长率并不完全一致
D. 从1~4月来看,该省在2018年快递业务收入同比增长率逐月增长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】箱子中有形状、大小都相同的3只红球,2只白球,从中一次摸出2只球.
(1)求摸到的2只球颜色不同的概率:
(2)求摸到的2只球中至少有1只红球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}满足![]() .
.
(1)若![]() ,求证:存在
,求证:存在![]() (a,b,c为常数),使数列
(a,b,c为常数),使数列![]() 是等比数列,并求出数列{an}的通项公式;
是等比数列,并求出数列{an}的通项公式;
(2)若an 是一个等差数列{bn}的前n项和,求首项a1的值与数列{bn}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某亲子游戏结束时有一项抽奖活动,抽奖规则是:盒子里面共有4个小球,小球上分别写有0,1,2,3的数字,小球除数字外其他完全相同,每对亲子中,家长先从盒子中取出一个小球,记下数字后将小球放回,孩子再从盒子中取出一个小球,记下小球上数字将小球放回.抽奖活动的奖励规则是:①若取出的两个小球上数字之积大于4,则奖励飞机玩具一个;②若取出的两个小球上数字之积在区间上![]() ,则奖励汽车玩具一个;③若取出的两个小球上数字之积小于1,则奖励饮料一瓶.
,则奖励汽车玩具一个;③若取出的两个小球上数字之积小于1,则奖励饮料一瓶.
(1)求每对亲子获得飞机玩具的概率;
(2)试比较每对亲子获得汽车玩具与获得饮料的概率,哪个更大?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com