
(本小题满分14分)已知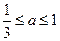 ,若函数
,若函数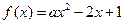 在区间
在区间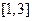 上
上
的最大值为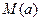 ,最小值为
,最小值为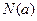 ,令
,令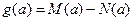 .
.
(1)求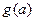 的函数表达式;
的函数表达式;
(2)判断函数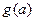 在区间
在区间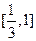 上的单调性,并求出
上的单调性,并求出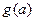 的最小值.
的最小值.
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:解答题
(理数)(12分)某商场销售 某种商品的经验表明,该商品每日的销售量
某种商品的经验表明,该商品每日的销售量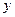 (单位:千克)与销售价格
(单位:千克)与销售价格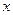 (单位:元/千克)满
(单位:元/千克)满 足关系式
足关系式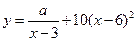 ,其中
,其中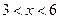 ,
,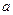 为常数,已知销售价格为5元/千克时,每日可售出该商品11千克
为常数,已知销售价格为5元/千克时,每日可售出该商品11千克
(Ⅰ) 求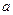 的值;
的值;
(Ⅱ) 若该商品的成品为3元/千克, 试确定销售价格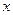 的值,使商场每日销售该
的值,使商场每日销售该 商品所获得的利润最大.
商品所获得的利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题11分)如图,矩形ABCD中,AB=6,BC=2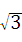 ,点O是AB的中点,点P在AB的延长线
,点O是AB的中点,点P在AB的延长线 上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点
上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点 出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).
出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).
(1)当等边△EFG的边FG恰好经过点C时,求运动时间t的值;
(2)在整个运动过程中,设等边△EFG和矩形ABCD重叠部分的面积 为S,求出S与t之间的函数关系式和相应的自变量t的取值范围;
为S,求出S与t之间的函数关系式和相应的自变量t的取值范围;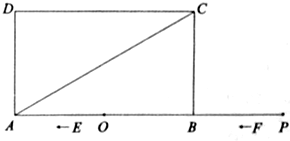
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知二次函数 的图象与x轴有两个不同的公共点,且
的图象与x轴有两个不同的公共点,且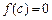 ,当
,当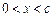 时,恒有
时,恒有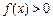 .
.
(1)当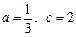 时,求不等式
时,求不等式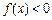 的解集;
的解集;
(2)若以二次函数的图象与坐标轴的三个交点为顶点的三角形的面积为8,且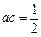 ,求a的值;
,求a的值;
(3)若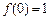 ,且
,且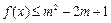 对所有
对所有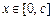 恒成立,求正实数m的最小值.
恒成立,求正实数m的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某地方政府为地方电子工业发展,决定对某一进口电子产品征收附加税。已知这种电子产品国内市场零售价为每件250元,每年可销售40万件,若政府征收附加税率为t元时,则每年减少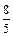 y万件。
y万件。
(1)收入表示为征收附加税率的函数;
(2)在 该项经营中每年征收附加税金不低于600万元,那么附加税率应控制在什么范围?
该项经营中每年征收附加税金不低于600万元,那么附加税率应控制在什么范围?
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
曲线f(x)=x3+x﹣2在p0处的切线平行于直线y=4x﹣1,则p0的坐标为( )
| A.(1,0) | B.(2,8) |
| C.(1,0)或(﹣1,﹣4) | D.(2,8)或(﹣1,﹣4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com