
【题目】已知点![]() 直线AM,BM相交于点M,且它们的斜率之和为2.
直线AM,BM相交于点M,且它们的斜率之和为2.
(1)设![]() 且
且![]() ,求
,求![]() 的表达式,并写出函数
的表达式,并写出函数![]() 的定义域;
的定义域;
(2)判断函数![]() 的奇偶性?并给出证明;
的奇偶性?并给出证明;
(3)试用函数单调性的定义证明:![]() 在定义域上不是增函数,但在(0,1)∪(1,+
在定义域上不是增函数,但在(0,1)∪(1,+![]() )上为增函数.
)上为增函数.
【答案】(1)![]() ,定义域为{
,定义域为{![]() 丨
丨![]() 且
且![]() };(2)奇函数,证明见解析;(3)证明见解析.
};(2)奇函数,证明见解析;(3)证明见解析.
【解析】
(1)设![]() 由题意求出
由题意求出![]() ,然后列出表达式,再求出满足表达式的定义域;
,然后列出表达式,再求出满足表达式的定义域;
(2)利用函数奇偶性的定义直接证明判断;
(3)举出反例证明函数在整个定义域上不是增函数,然后利用函数单调性的定义证明在(0,1)∪(1,+![]() )上为增函数.
)上为增函数.
(1)设![]() ,由题意可得
,由题意可得![]() ,则
,则![]() ,
,
化简得得:![]() ,由
,由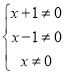 ,可得
,可得![]() 且
且![]() ,所以可得函数表达式为:
,所以可得函数表达式为:![]() ,定义域为{
,定义域为{![]() 丨
丨![]() 且
且![]() };
};
(2)由(1)得函数定义域为{![]() 丨
丨![]() 且
且![]() },关于原点对称,
},关于原点对称,
所以由![]() ,可得
,可得![]() 在定义域上是奇函数;
在定义域上是奇函数;
(3)取![]() ,
,
则由![]() ,
,![]() 可得
可得![]() 在定义域上不是增函数,
在定义域上不是增函数,
设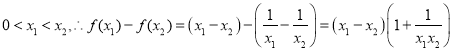 ,
,
显然无论![]() ,或者
,或者![]() 或者
或者![]() 都有
都有![]() ,即
,即![]()
从而![]() 在(0,1)∪(1,+
在(0,1)∪(1,+![]() )上为增函数.
)上为增函数.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2﹣4y+1=0,点M(﹣1,﹣1),从圆C外一点P向该圆引一条切线,记切点为T.
(1)若过点M的直线l与圆交于A,B两点且|AB|=2![]() ,求直线l的方程;
,求直线l的方程;
(2)若满足|PT|=|PM|,求使|PT|取得最小值时点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2016·贵阳第二次联考)在△ABC中,角A,B,C的对边分别为a,b,c,向量m=(a+b,sin A-sin C),向量n=(c,sin A-sin B),且m∥n.
(1)求角B的大小;
(2)设BC的中点为D,且AD=![]() ,求a+2c的最大值及此时△ABC的面积.
,求a+2c的最大值及此时△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一2班学生每周用于数学学习的时间![]() (单位:
(单位:![]() )与数学成绩
)与数学成绩![]() (单位:分)之间有如下数据:
(单位:分)之间有如下数据:
| 24 | 15 | 23 | 19 | 16 | 11 | 20 | 16 | 17 | 13 |
| 92 | 79 | 97 | 89 | 64 | 47 | 83 | 68 | 71 | 59 |
某同学每周用于数学学习的时间为18小时,试预测该生数学成绩.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() x3+
x3+![]() x2-ax-a,x∈R,其中a>0.
x2-ax-a,x∈R,其中a>0.
(1)求函数f(x)的单调区间;
(2)若函数f(x)在区间(-2,0)内恰有两个零点,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C的顶点在坐标原点,焦点F在x轴上,抛物线C上一点![]() 到焦点F的距离为
到焦点F的距离为![]() .
.
![]() Ⅰ
Ⅰ![]() 求抛物线C的标准方程;
求抛物线C的标准方程;
![]() Ⅱ
Ⅱ![]() 设点
设点![]() ,过点
,过点![]() 的直线l与抛物线C相交于A,B两点,记直线MA与直线MB的斜率分别为
的直线l与抛物线C相交于A,B两点,记直线MA与直线MB的斜率分别为![]() ,
,![]() ,证明:
,证明:![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com