
 16),f(
16),f( ),f(
),f( )的大小关系为________(用“<”连接)
)的大小关系为________(用“<”连接) )<f(log
)<f(log 16)
16)
 )<0,可分析出f(x)在(π,
)<0,可分析出f(x)在(π, ]上单调递减,从而使问题解决.
]上单调递减,从而使问题解决. 16=
16=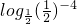 =-4,
=-4, 16)=f(-4)=f(4);
16)=f(-4)=f(4); )时,sinx<0,cosx<0,
)时,sinx<0,cosx<0, ]上单调递减,
]上单调递减, )=sin
)=sin +
+ cos
cos =-
=- -
- ×
× <0,
<0, <x≤
<x≤ ,f′(x)<0,
,f′(x)<0, 时,f′(x)<0,
时,f′(x)<0, ]上单调递减.
]上单调递减. <4<
<4< ,
, )>f(4)>f(
)>f(4)>f( );
); )<f(log
)<f(log 16)<f(
16)<f( ).
). ]上单调递减是关键,也是难点,属于难题.
]上单调递减是关键,也是难点,属于难题. 

 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
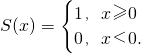 例如要表示分段函数
例如要表示分段函数 可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x).
可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x).查看答案和解析>>
科目:高中数学 来源:2012-2013学年北京市朝阳区陈经纶中学高一(上)期中数学试卷(解析版) 题型:解答题
 例如要表示分段函数
例如要表示分段函数 可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x).
可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x).查看答案和解析>>
科目:高中数学 来源:2012-2013学年北京市朝阳区陈经纶中学高一(上)期中数学试卷(解析版) 题型:解答题
 例如要表示分段函数
例如要表示分段函数 可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x).
可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com