
【题目】下列函数中,既是偶函数又在区间(﹣∞,0)上单调递增的是( )
A.f(x)= ![]()
B.f(x)=x2+1
C.f(x)=x
D.f(x)=2x
 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的方程为
的方程为![]() ,在以原点为极点,
,在以原点为极点, ![]() 轴的非负关轴为极轴的极坐标系中,直线
轴的非负关轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)将![]() 上的所有点的横坐标和纵坐标分别伸长到原来的2倍和
上的所有点的横坐标和纵坐标分别伸长到原来的2倍和![]() 倍后得到曲线
倍后得到曲线![]() ,求曲线
,求曲线![]() 的参数方程;
的参数方程;
(2)若![]() 分别为曲线
分别为曲线![]() 与直线
与直线![]() 的两个动点,求
的两个动点,求![]() 的最小值以及此时点
的最小值以及此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
平面直角坐标系中,直线![]() 的参数方程为
的参数方程为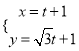 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的极坐标方程与曲线
的极坐标方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知与直线![]() 平行的直线
平行的直线![]() 过点
过点![]() ,且与曲线
,且与曲线![]() 交于
交于![]() 两点,试求
两点,试求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中
①函数f(x)=( ![]() )x的递减区间是(﹣∞,+∞)
)x的递减区间是(﹣∞,+∞)
②已知函数f(x)的定义域为(0,1),则函数f(x+1)的定义域为(1,2);
③已知(x,y)映射f下的象是(x+y,x﹣y),那么(4,2)在f下的原象是(3,1).
其中正确命题的序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
频数 | 6 | 26 | 38 | 22 | 8 |
(1)作出这些数据的频率分布直方图;
(2)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);
(3)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次数学考试试题中共有![]() 道选择题,每道选择题都有
道选择题,每道选择题都有![]() 个选项,其中仅有一个是正确的.评分标准规定:“每题只选
个选项,其中仅有一个是正确的.评分标准规定:“每题只选![]() 项,答对得
项,答对得![]() 分,不答或答错得
分,不答或答错得![]() 分.”某考生每道题都给了一个答案,已确定有
分.”某考生每道题都给了一个答案,已确定有![]() 道题的答案是正确的,而其余题中,有两道题都可判断出两个选项是错误的有一道题可以判断一个选项是错误的,还有一道题因不理解题意只能乱猜,试求出该考生:
道题的答案是正确的,而其余题中,有两道题都可判断出两个选项是错误的有一道题可以判断一个选项是错误的,还有一道题因不理解题意只能乱猜,试求出该考生:
(Ⅰ)得![]() 分的概率;
分的概率;
(Ⅱ)所得分数![]() 的数学期望.
的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com