
【题目】已知口袋里装有4个大小相同的小球,其中两个标有数字1,两个标有数字2.
(1)从口袋里任意取一球,求取到标有数字2的球的概率;
(2)第一次从口袋里任意取一球,放回口袋里后第二次再任意取一球,记第一次与第二次取到小球上的数字之和为![]() .当
.当![]() 为何值时,其发生的概率最大?说明理由.
为何值时,其发生的概率最大?说明理由.
【答案】(1)![]() ;(2)数字和为3时概率最大,理由详见解析.
;(2)数字和为3时概率最大,理由详见解析.
【解析】
(1)利用古典概型的概率计算公式即可求解.
(2)设标号为1的球为![]() ,
,![]() ,标号为2的球为
,标号为2的球为![]() ,
,![]() ,采用列举法求出所有基本事件个数,然后分别求出数字和为2、3、4的基本事件个数,利用古典概型的概率计算公式求出各自的概率即可求解.
,采用列举法求出所有基本事件个数,然后分别求出数字和为2、3、4的基本事件个数,利用古典概型的概率计算公式求出各自的概率即可求解.
解:(1)4个球中标有数字2的球有2个,故所求概率为![]() ,
,
(2)设标号为1的球为![]() ,
,![]() ,标号为2的球为
,标号为2的球为![]() ,
,![]() .
.
所有基本事件包括:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,共16种.
,共16种.
设事件![]() 表示数字和为2,
表示数字和为2,
包括:![]() ,
,![]() ,
,![]() ,
,![]() ,共4种,
,共4种,
故有![]() .
.
设事件![]() 表示数字和为3,
表示数字和为3,
包括:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,共8种,
,共8种,![]() .
.
设事件![]() 表示数字和为4,
表示数字和为4,
包括:![]() ,
,![]() ,
,![]() ,
,![]() ,共4种,
,共4种,
故![]() .
.
![]() 数字和为3时概率最大.
数字和为3时概率最大.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,给出以下四个命题:
,给出以下四个命题:
①![]() 的图象关于
的图象关于![]() 轴对称;
轴对称;
②![]() 在
在![]() 上是减函数;
上是减函数;
③![]() 是周期函数;
是周期函数;
④![]() 在
在![]() 上恰有两个零点.
上恰有两个零点.
其中真命题的序号是______.(请写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() ,曲线
,曲线![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() 的极坐标方程为
的极坐标方程为![]() ,若
,若![]() 分别与
分别与![]() 交于异于极点的
交于异于极点的![]() 两点,求
两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某水果批发商经销某种水果(以下简称![]() 水果),购入价为300元/袋,并以360元/袋的价格售出,若前8小时内所购进的
水果),购入价为300元/袋,并以360元/袋的价格售出,若前8小时内所购进的![]() 水果没有售完,则批发商将没售完的
水果没有售完,则批发商将没售完的![]() 水果以220元/袋的价格低价处理完毕(根据经验,2小时内完全能够把
水果以220元/袋的价格低价处理完毕(根据经验,2小时内完全能够把![]() 水果低价处理完,且当天不再购入).该水果批发商根据往年的销量,统计了100天
水果低价处理完,且当天不再购入).该水果批发商根据往年的销量,统计了100天![]() 水果在每天的前8小时内的销售量,制成如下频数分布条形图.
水果在每天的前8小时内的销售量,制成如下频数分布条形图.
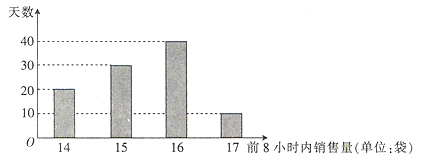
记![]() 表示
表示![]() 水果一天前8小时内的销售量,
水果一天前8小时内的销售量,![]() 表示水果批发商一天经营
表示水果批发商一天经营![]() 水果的利润,
水果的利润,![]() 表示水果批发商一天批发
表示水果批发商一天批发![]() 水果的袋数.
水果的袋数.
(1)若![]() ,求
,求![]() 与
与![]() 的函数解析式;
的函数解析式;
(2)假设这100天中水果批发商每天购入![]() 水果15袋或者16袋,分别计算该水果批发商这100天经营
水果15袋或者16袋,分别计算该水果批发商这100天经营![]() 水果的利润的平均数,以此作为决策依据,每天应购入
水果的利润的平均数,以此作为决策依据,每天应购入![]() 水果15袋还是16袋?
水果15袋还是16袋?
查看答案和解析>>
科目:高中数学 来源: 题型:
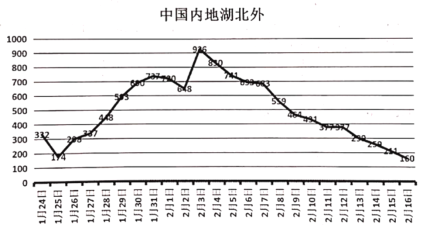
【题目】2019年春节前后,中国爆发新型冠状病毒(SARS-Cov-2)如图所示为1月24日至2月16日中国内地(除湖北以外的)感染新型冠状病毒新增人数的折线图,为了预测分析数据的变化规律,建立了![]() 与时间变量
与时间变量![]() 的不同时间段的两个线性回归模型.根据1月24日至2月3日的数据(时间变量
的不同时间段的两个线性回归模型.根据1月24日至2月3日的数据(时间变量![]() 的值依次为1,2,3,4,5,6,7,8,9,10,11)建立模型①:
的值依次为1,2,3,4,5,6,7,8,9,10,11)建立模型①:![]() ;根据2月4日至2月16日的数据(时间变量
;根据2月4日至2月16日的数据(时间变量![]() 的值依次为12,13,14,15,16,17,18,19,20,21,22,23,24)建立模型②:
的值依次为12,13,14,15,16,17,18,19,20,21,22,23,24)建立模型②:![]() .
.
1月 24日 | 1月 25日 | 1月 26日 | 1月 27日 | 1月 28日 | 1月 29日 | 1月 30日 | 1月 31日 | 2月 1日 | 2月 2日 | 2月 3日 |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
332 | 174 | 298 | 337 | 448 | 593 | 690 | 737 | 720 | 648 | 926 |
2月 4日 | 2月 5日 | 2月 6日 | 2月 7日 | 2月 8日 | 2月 9日 | 2月 10日 | 2月 11日 | 2月 12日 | 2月 13日 | 2月 14日 | 2月 15日 | 2月 16日 |
12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
830 | 741 | 693 | 683 | 559 | 464 | 431 | 377 | 377 | 299 | 259 | 211 | 160 |
(1)求出两个回归直线方程;(计算结果取整数)
(2)中国政府为了人民的生命安全,听取专家意见,了解了病毒信息,并迅速做出一系列的隔离防护措施,但新冠状病毒在世界范围内爆发时,某些欧美国家采取放任的态度,不治疗、不隔离、不检测,甚至不公布,请你用以上数据说明采取一系列措施的必要性,不采取措施的后果.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]()
参考公式: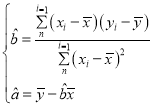 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,直线
,直线![]() 过右焦点
过右焦点![]() ,过点
,过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点(均不为顶点)
两点(均不为顶点)
(1)求椭圆![]() 的方程;
的方程;
(2)已知![]() 是椭圆
是椭圆![]() 的右顶点,直线
的右顶点,直线![]() ,若直线
,若直线![]() 与直线
与直线![]() 交于点
交于点![]() 直线
直线![]() 与直线
与直线![]() 交于点
交于点![]() ,试判断
,试判断![]() 是否为定值,若是,求出定值,若不是请说明理由.
是否为定值,若是,求出定值,若不是请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为4.且过点
的焦距为4.且过点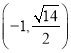 .
.
(1)求椭圆E的方程;
(2)设![]() ,
,![]() ,
,![]() ,过B点且斜率为
,过B点且斜率为![]() 的直线l交椭圆E于另一点M,交x轴于点Q,直线AM与直线
的直线l交椭圆E于另一点M,交x轴于点Q,直线AM与直线![]() 相交于点P.证明:
相交于点P.证明:![]() (O为坐标原点).
(O为坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长为1的正方体![]() 中,E,F分别为线段CD和
中,E,F分别为线段CD和![]() 上的动点,且满足
上的动点,且满足![]() ,则四边形
,则四边形![]() 所围成的图形(如图所示阴影部分)分别在该正方体有公共顶点的三个面上的正投影的面积之和( )
所围成的图形(如图所示阴影部分)分别在该正方体有公共顶点的三个面上的正投影的面积之和( )

A. 有最小值![]() B. 有最大值
B. 有最大值![]() C. 为定值3D. 为定值2
C. 为定值3D. 为定值2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com