
分析 (1)若函数的定义域为R,则(m2-1)x2-(1-m)x+1>0对x∈R恒成立,进而可得实数m的取值范围;
(2)若函数的值域为R,则g(x)=(m2-1)x2-(1-m)x+1的值域包含(0,+∞),进而可得实数m的取值范围.
解答 解:(1)由题知(m2-1)x2-(1-m)x+1>0对x∈R恒成立.
(I)当m2-1=0时,若m=1,有1>0恒成立,符合题意:
若m=-1,有$x<\frac{1}{2}$,不合题意.
(II)当m2-1≠0即m≠±1时,
有$\left\{\begin{array}{l}{m^2}-1>0⇒m>1或m<-1\\△={(1-m)^2}-4({m^2}-1)<0⇒m>1或m<-\frac{5}{3}\end{array}\right.$解得:m>1或$m<-\frac{5}{3}$;
∴由(I)(II)可知$m∈(-∞,-\frac{5}{3})∪[1,+∞)$.
(2)由题意,g(x)=(m2-1)x2-(1-m)x+1的值域包含(0,+∞),
(I)当m2-1=0时,若m=1,有g(x)=1,不合题意;
若m=-1,则g(x)=-2x+1,符合题意.
(II)当m2-1≠0即m≠±1时
有$\left\{\begin{array}{l}{m^2}-1>0\\△≥0\end{array}\right.$解得:$-\frac{5}{3}≤m<-1$
∴由(I)(II)可知$m∈[-\frac{5}{3},-1]$.
点评 本题考查的知识点是函数恒成立问题,二次函数的图象和性质,对数函数的图象和性质,难度中档.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{2015}{2016}$ | B. | $\frac{2015}{1008}$ | C. | $\frac{2015}{672}$ | D. | $\frac{2015}{336}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
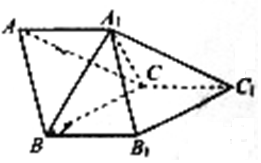 如图所示,三棱柱ABC-A1B1C1中,AA1⊥BC,A1B⊥BB1,若AB=2,AC=$\sqrt{3}$,BC=$\sqrt{7}$,则下列结论正确的是( )
如图所示,三棱柱ABC-A1B1C1中,AA1⊥BC,A1B⊥BB1,若AB=2,AC=$\sqrt{3}$,BC=$\sqrt{7}$,则下列结论正确的是( )| A. | :当AA1=$\frac{\sqrt{42}}{7}$时,三棱柱ABC-A1B1C1体积取得最大值,最大值为$\frac{3\sqrt{7}}{7}$ | |
| B. | :当AA1=$\frac{6}{7}$时,三棱柱ABC-A1B1C1体积取得最大值,最大值为$\frac{3\sqrt{7}}{7}$ | |
| C. | :当AA1=$\frac{\sqrt{42}}{7}$时,三棱柱ABC-A1B1C1体积取得最大值,最大值为$\frac{6}{7}$$\sqrt{7}$ | |
| D. | :当AA1=$\frac{6}{7}$时,三棱柱ABC-A1B1C1体积取得最大值,最大值为$\frac{6}{7}$$\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
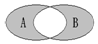 如图所示,A、B是两个非空集合,定义A*B表示阴影部分集合,若集合A={x|y=$\sqrt{3x-{x^2}}$,x,y∈R},B={y|y=2x,x>0},则A*B=( )
如图所示,A、B是两个非空集合,定义A*B表示阴影部分集合,若集合A={x|y=$\sqrt{3x-{x^2}}$,x,y∈R},B={y|y=2x,x>0},则A*B=( )| A. | [0,+∞) | B. | [0,1]∪(3,+∞) | C. | [0,1)∪[3,+∞) | D. | (1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com