
【题目】已知函数![]() ,其中
,其中![]() .
.
(Ⅰ)若![]() ,求函数
,求函数![]() 的极值;
的极值;
(Ⅱ)设![]() .若
.若![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,过点
,过点![]() 的直线交抛物线于
的直线交抛物线于![]() ,
,![]() 两点,点
两点,点![]() 在准线
在准线![]() 上的投影为
上的投影为![]() ,若
,若![]() 是抛物线上一点,且
是抛物线上一点,且![]() .
.
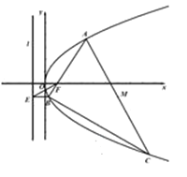
(1)证明:直线![]() 经过
经过![]() 的中点
的中点![]() ;
;
(2)求![]() 面积的最小值及此时直线
面积的最小值及此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
,![]() 为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线
为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线![]() 是圆心在极轴上,且经过极点的圆.已知曲线
是圆心在极轴上,且经过极点的圆.已知曲线![]() 上的点M
上的点M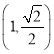 对应的参数
对应的参数![]() ,射线
,射线![]() 与曲线
与曲线![]() 交于点
交于点![]() .
.
(1)求曲线![]() ,
,![]() 的直角坐标方程;
的直角坐标方程;
(2)若点A,B为曲线![]() 上的两个点且
上的两个点且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,如图,已知椭圆E:
中,如图,已知椭圆E:![]() 的左、右顶点分别为
的左、右顶点分别为![]() 、
、![]() ,上、下顶点分别为
,上、下顶点分别为![]() 、
、![]() .设直线
.设直线![]() 倾斜角的余弦值为
倾斜角的余弦值为![]() ,圆
,圆![]() 与以线段
与以线段![]() 为直径的圆关于直线
为直径的圆关于直线![]() 对称.
对称.

(1)求椭圆E的离心率;
(2)判断直线![]() 与圆
与圆![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(3)若圆![]() 的面积为
的面积为![]() ,求圆
,求圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某动漫影视制作公司长期坚持文化自信,不断挖掘中华优秀传统文化中的动漫题材,创作出一批又一批的优秀动漫影视作品,获得市场和广大观众的一致好评,同时也为公司赢得丰厚的利润.该公司![]() 年至
年至![]() 年的年利润
年的年利润![]() 关于年份代号
关于年份代号![]() 的统计数据如下表(已知该公司的年利润与年份代号线性相关).
的统计数据如下表(已知该公司的年利润与年份代号线性相关).
年份 |
|
|
|
|
|
|
|
年份代号 |
|
|
|
|
|
|
|
年利润 |
|
|
|
|
|
|
|
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程,并预测该公司
的线性回归方程,并预测该公司![]() 年(年份代号记为
年(年份代号记为![]() )的年利润;
)的年利润;
(Ⅱ)当统计表中某年年利润的实际值大于由(Ⅰ)中线性回归方程计算出该年利润的估计值时,称该年为![]() 级利润年,否则称为
级利润年,否则称为![]() 级利润年.将(Ⅰ)中预测的该公司
级利润年.将(Ⅰ)中预测的该公司![]() 年的年利润视作该年利润的实际值,现从
年的年利润视作该年利润的实际值,现从![]() 年至
年至![]() 年这
年这![]() 年中随机抽取
年中随机抽取![]() 年,求恰有
年,求恰有![]() 年为
年为![]() 级利润年的概率.
级利润年的概率.
参考公式: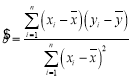 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】凤梨穗龙眼原产厦门,是厦门市的名果,栽培历史已有100多年.龙眼干的级别按直径![]() 的大小分为四个等级(如下表).
的大小分为四个等级(如下表).
|
|
|
|
|
级别 | 三级品 | 二级品 | 一级品 | 特级品 |
某商家为了解某农场一批龙眼干的质量情况,随机抽取了100个龙眼干作为样本(直径分布在区间![]() ),统计得到这些龙眼干的直径的频数分布表如下:
),统计得到这些龙眼干的直径的频数分布表如下:
|
|
|
|
|
|
频数 | 1 |
| 29 |
| 7 |
用分层抽样的方法从样本的一级品和特级品中抽取6个,其中一级品有2个.
(1)求![]() 、
、![]() 的值,并估计这批龙眼干中特级品的比例;
的值,并估计这批龙眼干中特级品的比例;
(2)已知样本中的100个龙眼干约500克,该农场有500千克龙眼干待出售,商家提出两种收购方案:
方案![]() :以60元/千克收购;
:以60元/千克收购;
方案![]() :以级别分装收购,每袋100个,特级品40元/袋、一级品30元/袋、二级品20元/袋、三级品10元/袋.
:以级别分装收购,每袋100个,特级品40元/袋、一级品30元/袋、二级品20元/袋、三级品10元/袋.
用样本的频率分布估计总体分布,哪个方案农场的收益更高?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了解全校学生的体重情况,从全校学生中随机抽取了100 人的体重数据,得到如下频率分布直方图,以样本的频率作为总体的概率.
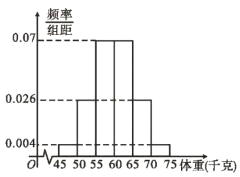
(1)估计这100人体重数据的平均值![]() 和样本方差
和样本方差![]() ;(结果取整数,同一组中的数据用该组区间的中点值作代表)
;(结果取整数,同一组中的数据用该组区间的中点值作代表)
(2)从全校学生中随机抽取3名学生,记![]() 为体重在
为体重在![]() 的人数,求
的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)由频率分布直方图可以认为,该校学生的体重![]() 近似服从正态分布
近似服从正态分布![]() .若
.若![]() ,则认为该校学生的体重是正常的.试判断该校学生的体重是否正常?并说明理由.
,则认为该校学生的体重是正常的.试判断该校学生的体重是否正常?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等边![]() 的边长为
的边长为![]() ,点
,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点,且满足
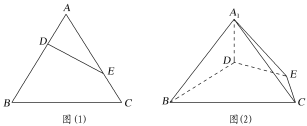
上的点,且满足![]() (如图(1)),将
(如图(1)),将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使二面角
的位置,使二面角![]() 成直二面角,连接
成直二面角,连接![]() ,
,![]() (如图(2)).
(如图(2)).
(1)求证:![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com