
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
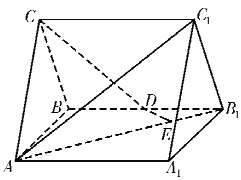
(I)若![]() 为
为![]() 上的一点,且
上的一点,且![]() 与直线
与直线![]() 垂直,求
垂直,求![]() 的值;
的值;
(Ⅱ)在(I)的条件下,设异面直线![]() 与
与![]() 所成的角为45°,求直线
所成的角为45°,求直线![]() 与平面
与平面![]() 成角的正弦值.
成角的正弦值.
【答案】(Ⅰ)见证明;(Ⅱ)![]()
【解析】
(Ⅰ)取![]() 中点
中点![]() ,连接
,连接![]() ,证明
,证明![]() ,即可说明
,即可说明![]() ,由底面为正方形,可求得
,由底面为正方形,可求得![]() ;
;
(Ⅱ)以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 为x轴、y轴、z轴,建立空间直角坐标系,求得各点的坐标,以及平面
为x轴、y轴、z轴,建立空间直角坐标系,求得各点的坐标,以及平面![]() 的法向量为
的法向量为![]() ,根据线面所成角的正弦值的公式即可求解。
,根据线面所成角的正弦值的公式即可求解。
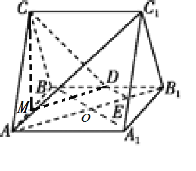
(Ⅰ)证明:取![]() 中点
中点![]() ,连接
,连接![]() ,有
,有![]() ,
,
因为![]() ,所以
,所以![]() ,
,
又因为三棱柱![]() 为直三棱柱,
为直三棱柱,
所以![]() ,
,
又因为![]() ,
,
所以![]() ,
,
又因为![]()
所以![]()
又因为![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() ,又因为
,又因为![]() 平面
平面![]() ,
,
所以![]() ,
,
因为![]() ,
,
所以![]() ,
,
连接![]() ,设
,设![]() ,因为
,因为![]() 为正方形,
为正方形,
所以![]() ,又因为
,又因为![]()
所以![]() ,
,
又因为![]() 为
为![]() 的中点,
的中点,
所以![]() 为
为![]() 的中点,
的中点,
所以![]() .
.
(Ⅱ)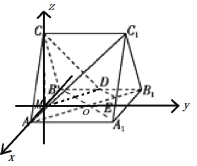
如图以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 为x轴、y轴、z轴,建立空间直角坐标系,
为x轴、y轴、z轴,建立空间直角坐标系,
设![]() ,由(Ⅰ)可知
,由(Ⅰ)可知![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则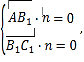 即
即![]()
则![]() 的一组解为
的一组解为![]() .
.
所以 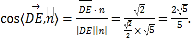
所以直线![]() 与平面
与平面![]() 成角的正弦值为
成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】在“五四青年节”到来之际,启东中学将开展一系列的读书教育活动.为了解高二学生读书教育情况,决定采用分层抽样的方法从高二年级![]() 四个社团中随机抽取12名学生参加问卷调査.已知各社团人数统计如下:
四个社团中随机抽取12名学生参加问卷调査.已知各社团人数统计如下:
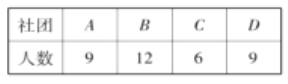
(1)若从参加问卷调查的12名学生中随机抽取2名,求这2名学生来自同一个社团的概率;
(2)在参加问卷调查的12名学生中,从来自![]() 三个社团的学生中随机抽取3名,用
三个社团的学生中随机抽取3名,用![]() 表示从
表示从![]() 社团抽得学生的人数,求
社团抽得学生的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险的基准保费为a元,在下一年续保时,实行费率浮动机制,保费与车辆发生道路交通事故出险的情况相联系,最终保费![]() 基准保费
基准保费![]() (
(![]() 与道路交通事故相联系的浮动比率),具体情况如下表:
与道路交通事故相联系的浮动比率),具体情况如下表:
交强险浮动因素和浮动费率比率表 | ||
类别 | 浮动因素 | 浮动比率 |
| 上一个年度未发生有责任道路交通事故 | 下浮 |
| 上两个年度未发生有责任道路交通事故 | 下浮 |
| 上三个及以上年度未发生有责任道路交通事故 | 下浮 |
| 上一个年度发生一次有责任不涉及死亡的道路交通事故 |
|
| 上一个年度发生两次及两次以上有责任不涉及死亡的道路交通事故 | 上浮 |
| 上一个年度发生有责任道路交通死亡事故 | 上浮 |
为了解某一品牌普通6座以下私家车的投保情况,随机抽取了100辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计如下表:
类型 |
|
|
|
|
|
|
数量 | 20 | 10 | 10 | 38 | 20 | 2 |
若以这100辆该品牌的投保类型的频率代替一辆车投保类型的概率,则随机抽取一辆该品牌车在第四年续保时的费用的期望为( )
A.a元B.![]() 元C.
元C.![]() 元D.
元D.![]() 元
元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象上所有点的横坐标缩短到原来的
的图象上所有点的横坐标缩短到原来的![]() 倍(纵坐标不变),再将所得的图象向左平移
倍(纵坐标不变),再将所得的图象向左平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图象.
的图象.
(1)写出函数![]() 的解析式;
的解析式;
(2)若对任意![]()
![]()
![]() ,
, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)求实数![]() 和正整数
和正整数![]() ,使得
,使得![]() 在
在![]() 上恰有
上恰有![]() 个零点.
个零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=4,AD=CD=2.将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D﹣ABC,如图2所示.
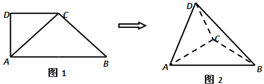
(Ⅰ)求证:BC⊥平面ACD;
(Ⅱ)求几何体D﹣ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】厂家在产品出厂前,需对产品做检验,厂家将一批产品发给商家时,商家按合同规定也需随机抽取一定数量的产品做检验,以决定是否接收这批产品.
(1)若厂家库房中(视为数量足够多)的每件产品合格的概率为 ![]() 从中任意取出 3件进行检验,求至少有
从中任意取出 3件进行检验,求至少有![]() 件是合格品的概率;
件是合格品的概率;
(2)若厂家发给商家![]() 件产品,其中有
件产品,其中有![]() 不合格,按合同规定 商家从这
不合格,按合同规定 商家从这![]() 件产品中任取
件产品中任取![]() 件,都进行检验,只有
件,都进行检验,只有![]() 件都合格时才接收这批产品,否则拒收.求该商家可能检验出的不合格产品的件数ξ的分布列,并求该商家拒收这批产品的概率.
件都合格时才接收这批产品,否则拒收.求该商家可能检验出的不合格产品的件数ξ的分布列,并求该商家拒收这批产品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学生在开学季准备销售一种文具套盒进行试创业,在一个开学季内,每售出1盒该产品获利50元,未售出的产品,每盒亏损30元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季进了160盒该产品,以![]() (单位:盒,
(单位:盒,![]() )表示这个开学季内的市场需求量,
)表示这个开学季内的市场需求量,![]() (单位:元)表示这个开学季内经销该产品的利润.
(单位:元)表示这个开学季内经销该产品的利润.
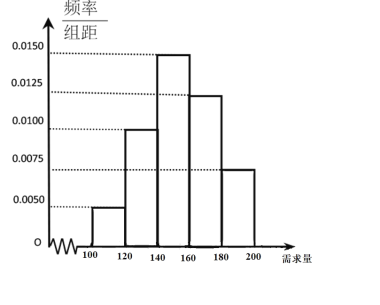
(1)根据直方图估计这个开学季内市场需求量![]() 的平均数和众数;
的平均数和众数;
(2)将![]() 表示为
表示为![]() 的函数;
的函数;
(3)以需求量的频率作为各需求量的概率,求开学季利润不少于4800元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市在节日期间进行有奖促销,凡在该超市购物满![]() 元的顾客,将获得一次摸奖机会,规则如下:一个袋子装有
元的顾客,将获得一次摸奖机会,规则如下:一个袋子装有![]() 只形状和大小均相同的玻璃球,其中两只是红色,三只是绿色,顾客从袋子中一次摸出两只球,若两只球都是红色,则奖励
只形状和大小均相同的玻璃球,其中两只是红色,三只是绿色,顾客从袋子中一次摸出两只球,若两只球都是红色,则奖励![]() 元;共两只球都是绿色,则奖励
元;共两只球都是绿色,则奖励![]() 元;若两只球颜色不同,则不奖励.
元;若两只球颜色不同,则不奖励.
(1)求一名顾客在一次摸奖活动中获得![]() 元的概率;
元的概率;
(2)记![]() 为两名顾客参与该摸奖活动获得的奖励总数额,求随机变量
为两名顾客参与该摸奖活动获得的奖励总数额,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com