练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设点P为有公共焦点F1 ， F2的椭圆和双曲线的一个交点，且cos∠F1PF2= ，椭圆的离心率为e1 ， 双曲线的离心率为e2 ， 若e2=2e1 ， 则e1=（ ）
    A.
    B.
    C.
    D.

    【答案】D
    【解析】解：设椭圆与双曲线的半长轴分别为a1 ， a2 ， 半焦距为c．e1= ，e2= ．设|PF1|=m，|PF2|=n，不妨设m＞n，
    则m+n=2a1 ， m﹣n=2a2 ．
    ∴m2+n2=2 +2 ，mn= ﹣ ．
    4c2=m2+n2﹣2mncos∠F1PF2 ，
    ∴4c2=2 +2 ﹣2（ ﹣ ）× ．
    化为：5c2= +4 ，
    ∴5= + ×4，又e2=2e1 ，
    ∴5= + ×4，e1∈（0，1）．
    则e1= ．
    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图所示，在四棱锥P﹣ABCD中，平面PAD⊥平面ABCD，AB∥DC，△PAD是等边三角形，已知BD=8，AD=4，AB=2DC=4 ．
    （1）设M是PC上的一点，求证：平面MBD⊥平面PAD；
    （2）求四棱锥P﹣ABCD的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知双曲线 =1（a＞0，b＞0）的左右焦点分别为F1 ， F2 ， |F1F2|=4，P是双曲线右支上的一点，F2P与y轴交于点A，△APF1的内切圆在边PF1上的切点为Q，若|PQ|=1，则双曲线的离心率是（ ）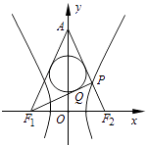
    A.3
    B.2
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}中，a1=1，a2=4，a3=10，若{an+1﹣an}是等比数列，则 i= ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}的前n项和为Sn ， 满足Sn=2﹣an（n∈N*）．数列{bn}满足（2n﹣1）bn+1﹣（2n+1）bn=0（n∈N*），且b1=1．
    （1）求数列{an}和{bn}的通项公式；
    （2）设cn=anbn ， 求数列{cn}的前n项和为Tn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点O为△ABC的外心，角A，B，C的对边分别满足a，b，c， （Ⅰ）若3 +4 +5 = ，求cos∠BOC的值；
    （Ⅱ）若 = ，求 的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知锐角△ABC中，角A、B、C所对的边分别为a、b、c，若a=2，b2+c2﹣bc=4，则△ABC的面积的取值范围是（ ）
    A.（ ， ]
    B.（0， ]
    C.（ ， ]
    D.（ ， ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，AB、CD是圆的两条平行弦，BE∥AC，BE交CD于E、交圆于F，过A点的切线交DC的延长线于P，PC=ED=1，PA=2．

    （1）求AC的长；
    （2）试比较BE与EF的长度关系．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在2015﹣2016赛季CBA联赛中，某队甲、乙两名球员在前10场比赛中投篮命中情况统计如下表（注：表中分数 ，N表示投篮次数，n表示命中次数），假设各场比赛相互独立．

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    甲

    乙

    根据统计表的信息：
    （1）从上述比赛中等可能随机选择一场，求甲球员在该场比赛中投篮命中率大于0.5的概率；
    （2）试估计甲、乙两名运动员在下一场比赛中恰有一人命中率超过0.5的概率；
    （3）在接下来的3场比赛中，用X表示这3场比赛中乙球员命中率超过0.5的场次，试写出X的分布列，并求X的数学期望．

    查看答案和解析>>

    同步练习册答案