
【题目】如图,在四棱锥S-ABCD中,四边形ABCD菱形,![]() ,平面
,平面![]() 平面 ABCD,
平面 ABCD,![]() .E,F 分别是线段 SC,AB 上的一点,
.E,F 分别是线段 SC,AB 上的一点, ![]() .
.
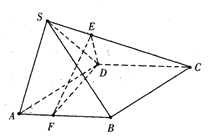
(1)求证:![]() 平面SAD;
平面SAD;
(2)求平面DEF与平面SBC所成锐二面角的正弦值.
【答案】(1)证明见解析
(2)![]()
【解析】
(1)先证明平行四边形AGEF,得到AG∥EF,再证明EF∥平面SAD;
(2)以OA,OB,OS所在直线为x,y,z轴,建立空间直角坐标系如图,求出平面DEF的法向量和平面SBC的一个法向量,利用向量的夹角公式求出二面角的余弦值,从而求出平面DEF与平面SBC所成锐二面角的正弦值.
(1)过点E作EG∥DC,如图,连接AG,因为![]() ,所以
,所以![]() ,
,
故EG∥CD,EG![]() ,由
,由![]() ,AF
,AF![]() ,
,
因为菱形ABCD,所以EG∥AF,EG=AF,
故平行四边形AGEF,所以AG∥EF,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)取AD中点O,等腰三角形SAD,故SO⊥AD,连接OB,
菱形ABCD,∠ADC=120°,所以OB⊥OA,
又平面SAD⊥平面ABCD所以SO⊥平面ABCD,
以OA,OB,OS所在直线为x,y,z轴,建立空间直角坐标系如图,
因为SA=SD=3![]() ,所以AD=AB=CD=6,SO=3,
,所以AD=AB=CD=6,SO=3,
∠ADC=120°,所以AF=2,OB![]() ,AO=OD=3,
,AO=OD=3,
所以A(3,0,0),D(﹣3,0,0),S(0,0,3),
F(2,![]() ,0),B(0,3
,0),B(0,3![]() ,0),C(﹣6,3
,0),C(﹣6,3![]() ,0),
,0),
又![]() (﹣2,
(﹣2,![]() ,﹣1),得E(﹣2,
,﹣1),得E(﹣2,![]() ,2),
,2),
所以![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面DEF的一个法向量为![]() ,
,
由 ,得
,得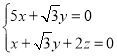 ,故
,故
设平面SBC的一个法向量为![]() ,
,
由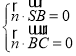 ,得
,得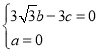 ,故
,故![]() ,
,
所以 ,
,
平面DEF与平面SBC所成锐二面角的正弦值为![]() .
.



 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:
【题目】以直角坐标系xOy的原点为极坐标系的极点,x轴的正半轴为极轴.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,P是
,P是![]() 上一动点,
上一动点,![]() ,Q的轨迹为
,Q的轨迹为![]() .
.
(1)求曲线![]() 的极坐标方程,并化为直角坐标方程,
的极坐标方程,并化为直角坐标方程,
(2)若点![]() ,直线l的参数方程为
,直线l的参数方程为![]() (t为参数),直线l与曲线
(t为参数),直线l与曲线![]() 的交点为A,B,当
的交点为A,B,当![]() 取最小值时,求直线l的普通方程.
取最小值时,求直线l的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 经过点
经过点![]() ,右焦点到直线
,右焦点到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)定义![]() 为
为![]() ,
,![]() 两点所在直线的斜率,若四边形
两点所在直线的斜率,若四边形![]() 为椭圆的内接四边形,且
为椭圆的内接四边形,且![]() ,
,![]() 相交于原点
相交于原点![]() ,且
,且![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() :
: ![]() 满足:
满足: ![]() ,
, ![]() 或1(
或1(![]() ).对任意
).对任意![]() ,都存在
,都存在![]() ,使得
,使得![]() .,其中
.,其中![]()
![]() 且两两不相等.
且两两不相等.
(I)若![]() .写出下列三个数列中所有符合题目条件的数列的序号;
.写出下列三个数列中所有符合题目条件的数列的序号;
①1,1,1,2,2,2;②1,1,1,1,2,2,2,2;③1,l,1,1,1,2,2,2,2
(Ⅱ)记![]() .若
.若![]() ,证明:
,证明: ![]() ;
;
(Ⅲ)若![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2|x+1|+|x-2|.
(1)求f(x)的最小值m;
(2)若a,b,c均为正实数,且满足a+b+c=m,求证:![]() +
+![]() +
+![]() ≥3.
≥3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某同学在素质教育基地通过自己设计、选料、制作,打磨出了一个作品,作品由三根木棒![]() ,
,![]() ,
,![]() 组成,三根木棒有相同的端点
组成,三根木棒有相同的端点![]() (粗细忽略不计),且
(粗细忽略不计),且![]() 四点在同一平面内,
四点在同一平面内,![]()
![]() ,
,![]() ,木棒
,木棒![]() 可绕点O任意旋转,设BC的中点为D.
可绕点O任意旋转,设BC的中点为D.
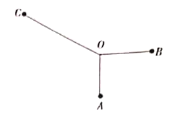
(1)当![]() 时,求OD的长;
时,求OD的长;
(2)当木棒OC绕点O任意旋转时,求AD的长的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com