
【题目】(1)利用“五点法”画出函数![]() 在长度为一个周期的闭区间的简图.
在长度为一个周期的闭区间的简图.
列表:
| |||||
x | |||||
y |
作图:
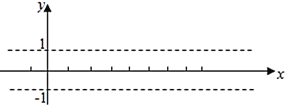
(2)并说明该函数图象可由![]() 的图象经过怎么变换得到的.
的图象经过怎么变换得到的.
(3)求函数![]() 图象的对称轴方程.
图象的对称轴方程.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】(1)由0,1,2,…,9这十个数字组成的无重复数字的四位数中,十位数字与千位数字之差的绝对值等于7的四位数的个数共有几种?
(2)我校高三学习雷锋志愿小组共有16人,其中一班、二班、三班、四班各4人,现在从中任选3人,要求这三人不能是同一个班级的学生,且在三班至多选1人,求不同的选取法的种数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有如下命题:①函数![]() 与
与![]() 的图象恰有三个交点;②函数
的图象恰有三个交点;②函数![]() 与
与![]() 的图象恰有一个交点;③函数
的图象恰有一个交点;③函数![]() 与
与![]() 的图象恰有两个交点;④函数
的图象恰有两个交点;④函数![]() 与
与![]() 的图象恰有三个交点,其中真命题为_____
的图象恰有三个交点,其中真命题为_____
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】酒驾是严重危害交通安全的违法行为.为了保障交通安全,根据国家有关规定:100mL血液中酒精含量低于20mg的驾驶员可以驾驶汽车,酒精含量达到20~79mg的驾驶员即为酒后驾车,80mg及以上认定为醉酒驾车.假设某驾驶员喝了一定量的酒后,其血液中的酒精含量上升到了1mg/mL.如果在停止喝酒以后,他血液中酒精含量会以每小时30%的速度减少,那么他至少经过几个小时才能驾驶汽车?( )(参考数据:lg0.2≈﹣0.7,1g0.3≈﹣0.5,1g0.7≈﹣0.15,1g0.8≈﹣0.1)
A.1B.3C.5D.7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com