
分析 (Ⅰ)先求出不等式|x-m|<1的解集,再由不等式|x-m|<1成立的充分不必要条件为$\frac{1}{3}$<x<$\frac{1}{2}$,确定m的取值范围.
(Ⅱ)利用绝对值不等式,结合|x-3|+|x-5|<a的解集不是空集,求实数a的取值范围.
解答 解:(Ⅰ)由不等式|x-m|<1得m-1<x<m+1,依题意{x|$\frac{1}{3}$<x<$\frac{1}{2}$}⊆{x|m-1<x<m+1},则$\left\{\begin{array}{l}{m-1≤\frac{1}{3}}\\{m+1≥\frac{1}{2}}\end{array}\right.$,
解得-$\frac{1}{2}≤m≤\frac{4}{3}$;5分
(Ⅱ)∵|x-3|+|x-5|≥|(x-3)-(x-5)|=2,
且|x-3|+|x-5|<a的解集不是空集,
∴a>2,即a的取值范围是(2,+∞).10分.
点评 本题考查充分不必要条件的应用,考查绝对值不等式,解题时要注意含绝对值不等式的解法和应用.


 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}<a<1$ | B. | a>1 | C. | $a<\frac{1}{3}$ | D. | a=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{8}$=1(x≠0) | B. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{8}$=1(x≠0) | C. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{8}$=1(y≠0) | D. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{8}$=1(y≠0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | -10 | C. | -20 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| ξ1 | 110 | 120 | 170 |
| P | m | 0.4 | n |
| X(次) | 0 | 1 | 2 |
| ξ2 | 41.2 | 117.6 | 204.0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
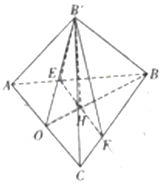 如图,等腰△ABC中,AB=BC=5,AC=6,点E,F分别在AB,BC上,AE=CF=$\frac{5}{4}$,O为AC边上的中点,EF交BO于点H,将△BEF沿EF折到△B′EF的位置,OB′=$\sqrt{10}$.
如图,等腰△ABC中,AB=BC=5,AC=6,点E,F分别在AB,BC上,AE=CF=$\frac{5}{4}$,O为AC边上的中点,EF交BO于点H,将△BEF沿EF折到△B′EF的位置,OB′=$\sqrt{10}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com