
【题目】在世界读书日期间,某地区调查组对居民阅读情况进行了调查,获得了一个容量为200的样本,其中城镇居民140人,农村居民60人.在这些居民中,经常阅读的城镇居民有100人,农村居民有30人.
(1)填写下面列联表,并判断能否有99%的把握认为经常阅读与居民居住地有关?
城镇居民 | 农村居民 | 合计 | |
经常阅读 | 100 | 30 | |
不经常阅读 | |||
合计 | 200 |
(2)从该地区城镇居民中,随机抽取5位居民参加一次阅读交流活动,记这5位居民中经常阅读的人数为![]() ,若用样本的频率作为概率,求随机变量
,若用样本的频率作为概率,求随机变量![]() 的期望.
的期望.
附: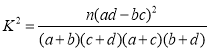 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若存在区间
,若存在区间![]() ,使得
,使得![]() ,则称函数
,则称函数![]() 为“可等域函数”,区间
为“可等域函数”,区间![]() 为函数
为函数![]() 的一个“可等域区间”.给出下列4个函数:
的一个“可等域区间”.给出下列4个函数:
①![]() ;②
;②![]() ; ③
; ③![]() ; ④
; ④![]() .
.
其中存在唯一“可等域区间”的“可等域函数”为( )
(A)①②③ (B)②③ (C)①③ (D)②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且满足bcosA﹣![]() asinB=0.
asinB=0.
(1)求A;
(2)已知a=2![]() ,B=
,B=![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为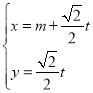 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,且曲线
,且曲线![]() 的左焦点
的左焦点![]() 在直线
在直线![]() 上.
上.
(Ⅰ)求![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的参数方程;
的参数方程;
(Ⅱ)求曲线![]() 的内接矩形的周长的最大值.
的内接矩形的周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产某种电子产品,每件产品不合格的概率均为![]() ,现工厂为提高产品声誉,要求在交付用户前每件产品都通过合格检验,已知该工厂的检验仪器一次最多可检验
,现工厂为提高产品声誉,要求在交付用户前每件产品都通过合格检验,已知该工厂的检验仪器一次最多可检验![]() 件该产品,且每 件产品检验合格与否相互独立.若每件产品均检验一次,所需检验费用较多,该工厂提出以下检 验方案:将产品每
件该产品,且每 件产品检验合格与否相互独立.若每件产品均检验一次,所需检验费用较多,该工厂提出以下检 验方案:将产品每![]() 个
个![]() 一组进行分组检验,如果某一组产品检验合格,则说明该组内产品均合格,若检验不合格,则说明该组内有不合格产品,再对该组内每一件产品单独进行检验,如此,每一组产品只需检验
一组进行分组检验,如果某一组产品检验合格,则说明该组内产品均合格,若检验不合格,则说明该组内有不合格产品,再对该组内每一件产品单独进行检验,如此,每一组产品只需检验![]() 次或
次或![]() 次.设该工厂生产
次.设该工厂生产![]() 件该产品,记每件产品的平均检验次 数为
件该产品,记每件产品的平均检验次 数为![]() .
.
(1)求![]() 的分布列及其期望;
的分布列及其期望;
(2)(i)试说明,当![]() 越小时,该方案越合理,即所需平均检验次数越少;
越小时,该方案越合理,即所需平均检验次数越少;
(ii)当![]() 时,求使该方案最合理时
时,求使该方案最合理时![]() 的值及
的值及![]() 件该产品的平均检验次数.
件该产品的平均检验次数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在明代程大位所著的《算法统宗》中有这样一首歌谣,“放牧人粗心大意,三畜偷偷吃苗青,苗主扣住牛马羊,要求赔偿五斗粮,三畜户主愿赔偿,牛马羊吃得异样.马吃了牛的一半,羊吃了马的一半.”请问各畜赔多少?它的大意是放牧人放牧时粗心大意,牛、马、羊偷吃青苗,青苗主人扣住牛、马、羊向其主人要求赔偿五斗粮食(1斗=10升),三畜的主人同意赔偿,但牛、马、羊吃的青苗量各不相同.马吃的青苗是牛的一半,羊吃的青苗是马的一半.问羊、马、牛的主人应该分别向青苗主人赔偿多少升粮食?( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】电影《厉害了,我的国》于2018年3月正式登陆全国院线,网友纷纷表示,看完电影热血沸腾“我为我的国家骄傲,我为我是中国人骄傲!”《厉害了,我的国》正在召唤我们每一个人,不忘初心,用奋斗书写无悔人生,小明想约甲、乙、丙、丁四位好朋友一同去看《厉害了,我的国》,并把标识为![]() 的四张电影票放在编号分别为1,2,3,4的四个不同的盒子里,让四位好朋友进行猜测:
的四张电影票放在编号分别为1,2,3,4的四个不同的盒子里,让四位好朋友进行猜测:
甲说:第1个盒子里放的是![]() ,第3个盒子里放的是
,第3个盒子里放的是![]()
乙说:第2个盒子里放的是![]() ,第3个盒子里放的是
,第3个盒子里放的是![]()
丙说:第4个盒子里放的是![]() ,第2个盒子里放的是
,第2个盒子里放的是![]()
丁说:第4个盒子里放的是![]() ,第3个盒子里放的是
,第3个盒子里放的是![]()
小明说:“四位朋友你们都只说对了一半”
可以预测,第4个盒子里放的电影票为_________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中AD∥BC,DA⊥AB,AD=2,AB=BC=1,CD![]() ,点E为PD中点.
,点E为PD中点.
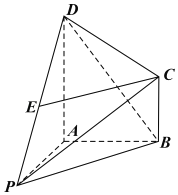
(1)求证:CE∥平面PAB;
(2)若PA=2,PD=2![]() ,∠PAB
,∠PAB![]() ,求平面PBD与平面ECD所成锐二面角的余弦值.
,求平面PBD与平面ECD所成锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com