
【题目】已知抛物线y2=2px(p>0),F为其焦点,过点(4,0)作垂直于x轴的直线交抛物线于A,B两点,△ABF的周长为18.
(1)求抛物线的方程;
(2)过抛物线上的定点 ![]() 作两条关于直线y=p对称的直线分别交抛物线于C,D两点,连接CD,判断直线CD的斜率是否为定值?并证明你的结论.
作两条关于直线y=p对称的直线分别交抛物线于C,D两点,连接CD,判断直线CD的斜率是否为定值?并证明你的结论.
【答案】
(1)解:依据题意,A,B两点的坐标为 ![]() ,
,
所以△ABF的周长为: ![]() ,
,
即 ![]() ,∴
,∴ ![]() ,
,
故抛物线方程为y2=4x.
(2)![]() 解:由(1)知M(1,2),由题意知MC,MD两直线关于直线y=2对称,则直线MC,MD的倾斜角互补,
解:由(1)知M(1,2),由题意知MC,MD两直线关于直线y=2对称,则直线MC,MD的倾斜角互补,
显然斜率均存在且不为0,设kMC=k,则kMD=﹣k,此时直线MC的方程为y﹣2=k(x﹣1), ![]() 将其代入y2=4x,并整理得:
将其代入y2=4x,并整理得: ![]() ,
,
设C(x1,y1),D(x2,y2),则由韦达定理可得: ![]() ,
,
所以 ![]() ,同理,将上式中的k换成﹣k,得
,同理,将上式中的k换成﹣k,得 ![]() ,
,
所以 ![]() ,
,
所以直线CD的斜率恒为﹣1.
【解析】1、根据题意求出A、B两点的坐标再利用△ABF的周长得到关于p的方程即得结果。
2、 由题意可设直线MC的斜率为k,MD的斜率为-k,可求得直线MC、MD的方程再与抛物线的方程联立求出交点坐标,进而可求得直线的斜率,从而可得到结论:直线CD的斜率恒为﹣1。


科目:高中数学 来源: 题型:
【题目】如图,在四棱柱ABCD﹣A1B1C1D1中,侧面ADD1A1⊥底面ABCD,D1A=D1D= ![]() ,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.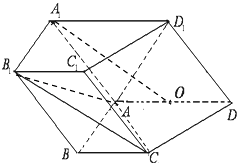
(Ⅰ)求证:A1O∥平面AB1C;
(Ⅱ)求锐二面角A﹣C1D1﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市随机抽取部分企业调查年上缴税收情况{单位万元,将所得数据绘制成频率分布直方图(如图),年上缴税收范围是[0,100]样本数据分组为[0,20),[20,40)[40,60)[60,80),[80,100)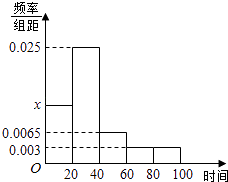
(1)求直方图中x的值;
(2)如果年上缴税收不少于60万元的企业可申请政策优惠,若共抽取企业1200个,试估计有多少企业可以申请政策优惠;
(3)从企业中任选4个,这4个企业年上缴税收少于20万元的个数记为X,求X的分布列和数学期望(以直方图中的频率作为概率)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水.天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸.若盆中积水深九寸,则平地降雨量是( )
(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸;③台体的体积公式V= ![]() )
)
A.2寸
B.3寸
C.4寸
D.5寸
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】广东佛山某学校参加暑假社会实践活动知识竞赛的学生中,得分在[80,90)中的有16人,得分在[90,100]中的有4人,用分层抽样的方法从得分在[80,100]的学生中抽取一个容量为5的样本,将该样本看成一个整体,从中任意选取2人,则其中恰有1人分数不低于90的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学人力资源部计划2016年招聘2名数学教师,共5名应聘者进入最后课堂实录环节.5名数学组评审专家给出评分如表:
评审专家/应聘老师 | 1 | 2 | 3 | 4 | 5 |
评审专家A | 93.0 | 90.0 | 88.5 | 89.5 | 82.5 |
评审专家B | 94.0 | 83.0 | 89.0 | 93.0 | 81.0 |
评审专家C | 91.0 | 85.0 | 81.5 | 88.0 | 81.0 |
评审专家D | 92.0 | 91.5 | 81.0 | 94.5 | 87.0 |
评审专家E | 95.5 | 91.0 | 90.0 | 95.5 | 88.5 |
(Ⅰ)若依据去掉一个最高分和一个最低分规则计算应聘老师成绩,试确定最终应聘成功的2名数学老师的序号;
(Ⅱ)在课堂实录环节,每名应聘老师都需要从5名评审专家中随机选取2名进行点评,且每名应聘老师的选择互不影响,设X表示评审专家A进行点评的次数,求X的分布列以及数学期望;
(Ⅲ)记评审专家A与评审专家B给出的评分的方差分别为 ![]() ,试比较
,试比较 ![]() 与
与 ![]() 的大小.(只需写出结论)
的大小.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定义在(0,+∞)上的单调函数f(x),对任意的x∈(0,+∞)都有f[f(x)﹣log2x]=3,若方程f(x)+f′(x)=a有两个不同的实数根,则实数a的取值范围是( )
A.(1,+∞)
B.(2+ ![]() ,+∞)
,+∞)
C.(2﹣ ![]() ,+∞)
,+∞)
D.(3,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,等腰梯形ABCD的底角 A等于60°,直角梯形 ADEF所在的平面垂直于平面ABCD,∠EDA=90°,且ED=AD=2AB=2AF.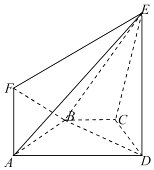
(1)证明:平面ABE⊥平面EBD;
(2)若三棱锥 A﹣BDE的外接球的体积为 ![]() ,求三棱锥 A﹣BEF的体积.
,求三棱锥 A﹣BEF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校随机抽取部分男生进行身体素质测试,获得掷实心球的成绩数据,整理得到数据分组及频率分布表,成绩在11.0米(精确到0.1米)以上(含)的男生为“优秀生”.
分组(米) | 频数 | 频率 |
[3.0,5.0) | 0.10 | |
[5.0,7.0) | 0.10 | |
[7.0,9.0) | 0.10 | |
[9.0,11.0) | 0.20 | |
[11.0,13.0) | 0.40 | |
[13.0,15.0) | 10 | |
合计 | 1.00 |
(Ⅰ)求参加测试的男生中“优秀生”的人数;
(Ⅱ)从参加测试男生的成绩中,根据表中分组情况,按分层抽样的方法抽取10名男生的成绩作为一个样本,再从该样本中任选2名男生的成绩,求至少选出1名男生的成绩不低于13.0米的概率;
(Ⅲ)若将这次测试的频率作为概率,从该校全体男生中随机抽取3人,记X表示3人中“优秀生”的人数,求X的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com