
【题目】已知函数![]() (
(![]() ,且
,且![]() ),且
),且![]() .
.
(1)求实数![]() 的值;
的值;
(2)判断函数![]() 的奇偶性并证明
的奇偶性并证明
(3)若函数![]() 有零点,求实数
有零点,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】已知![]() 是公差不为零的等差数列,满足
是公差不为零的等差数列,满足![]() ,且
,且![]() 、
、![]() 、
、![]() 成等比数列.
成等比数列.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 满足
满足![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)设等差数列![]() 的公差为
的公差为![]() ,由a3=7,且
,由a3=7,且![]() 、
、![]() 、
、![]() 成等比数列.可得
成等比数列.可得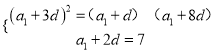 ,解之得即可得出数列
,解之得即可得出数列![]() 的通项公式;
的通项公式;
2)由(1)得![]() ,则
,则![]() ,由裂项相消法可求数列
,由裂项相消法可求数列![]() 的前
的前![]() 项和
项和![]() .
.
试题解析:(1)设数列![]() 的公差为
的公差为![]() ,且
,且![]() 由题意得
由题意得![]() ,
,
即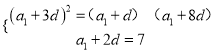 ,解得
,解得![]() ,
,
所以数列![]() 的通项公式
的通项公式![]() .
.
(2)由(1)得![]()
![]() ,
,
![]()
![]() .
.
【题型】解答题
【结束】
18
【题目】四棱锥![]() 的底面
的底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() 为正三角形.
为正三角形.
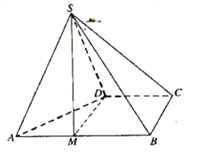
(1)点![]() 为棱
为棱![]() 上一点,若
上一点,若![]() 平面
平面![]() ,
,![]() ,求实数
,求实数![]() 的值;
的值;
(2)求点B到平面SAD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产甲、乙两种产品均需要![]() ,
,![]() 两种原料,已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产1吨甲、乙产品可获得利润分别为3万元、4万元,则该企业每天可获得最大利润为( )
两种原料,已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产1吨甲、乙产品可获得利润分别为3万元、4万元,则该企业每天可获得最大利润为( )
甲 | 乙 | 原料限额 | |
| 3 | 2 | 10 |
| 1 | 2 | 6 |
A. 10万元B. 12万元C. 13万元D. 14万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若函数![]() 为偶函数,求实数
为偶函数,求实数![]() 的值;
的值;
(2)若![]() ,
,![]() ,且函数
,且函数![]() 在
在![]() 上是单调函数,求实数
上是单调函数,求实数![]() 的值;
的值;
(3)若![]() ,若当
,若当![]() 时,总有
时,总有![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求![]() 的最小正周期;
的最小正周期;
(2)当![]() 时,
时,
(ⅰ)求函数![]() 的单调递减区间;
的单调递减区间;
(ⅱ)求函数![]() 的最大值最小值,并分别求出使该函数取得最大值最小值时的自变量
的最大值最小值,并分别求出使该函数取得最大值最小值时的自变量![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】最近几年,每年11月初,黄浦江上漂浮着的水葫芦便会迅速增长,严重影响了市容景观,为了解决这个环境问题,科研人员进行科研攻关,下图是科研人员在实验室池塘中观察水葫芦面积与时间的函数关系图像,假设其函数关系为指数函数,并给出下列说法:

①此指数函数的底数为![]() ;
;
②在第![]() 个月时,水葫芦的面积会超过
个月时,水葫芦的面积会超过![]() ;
;
③设水葫芦面积蔓延至![]() 所需的时间分别为
所需的时间分别为![]() ,则有
,则有![]() ;其中正确的说法有( )
;其中正确的说法有( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com