
分析 根据对数函数性质,f(x)=logax,当a>1时,函数为增函数,当0<a<1时,为减函数,且loga1=0,即可判断.
解答 解:根据对数函数性质,f(x)=logax,当a>1时,函数为增函数,当0<a<1时,为减函数,且loga1=0,
故${log}_{{5}^{3}}$<${log}_{{5}^{7}}$;
${log}_{{8}^{1}}$=${log}_{{7}^{1}}$;
${log}_{{\frac{1}{2}}^{5}}$<log${\;}_{\frac{1}{3}}$$\frac{1}{5}$,
ln0.3<0;
${log}_{{0.1}^{2}}$<0;
lg$\frac{1}{3}$<lg10.
故答案为:<,=,<,<,<,<
点评 本题考查了对数函数的图象和性质,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 20 | C. | 16 | D. | 32 |
查看答案和解析>>
科目:高中数学 来源:2017届广东佛山一中高三上学期月考一数学(理)试卷(解析版) 题型:选择题
已知全集U = R,集合 ,
, R│
R│ ≥
≥ ,下图中阴影部分所表示的集合为
,下图中阴影部分所表示的集合为

A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北冀州市高二理上月考三数学试卷(解析版) 题型:选择题
已知正四棱锥的各棱棱长都为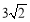 ,则正四棱锥的外接球的表面积为( )
,则正四棱锥的外接球的表面积为( )
A. B.
B.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com