
����Ŀ���ҹ�������������ȱˮ�Ĺ��ң�ij������Ϊ�˹��������Լ��ˮ���ƻ���������������ˮ�շѷ�������ȷ��һ������������ˮ����![]() ���֣���һλ���������ˮ��������
���֣���һλ���������ˮ��������![]() �IJ��ְ�ƽ���շѣ�����
�IJ��ְ�ƽ���շѣ�����![]() �IJ��ְ�����շѣ�Ϊ���˽������ˮ�����ͨ�������������ij��100λ����ÿ�˵��¾���ˮ������λ���֣��������ݰ���
�IJ��ְ�����շѣ�Ϊ���˽������ˮ�����ͨ�������������ij��100λ����ÿ�˵��¾���ˮ������λ���֣��������ݰ���![]() ��
�� ![]() ������
������ ![]() �ֳ�9�飬�Ƴ�����ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ.
�ֳ�9�飬�Ƴ�����ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ.
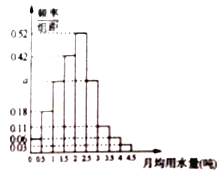
��1����ֱ��ͼ��![]() ��ֵ��
��ֵ��
��2������Ƶ����Ϊ���ʣ��Ӹó��о����������ȡ3�ˣ�����3�����¾���ˮ��������3�ֵ�����Ϊ![]() ����
����![]() �ķֲ�������ѧ����.
�ķֲ�������ѧ����.
��3������������ϣ��ʹ85%�ľ���ÿ�µ���ˮ����������![]() ���֣�������
���֣�������![]() ��ֵ����ȷ��0.01������˵������.
��ֵ����ȷ��0.01������˵������.
���𰸡���1��![]() ��2����������3��
��2����������3��![]()
�����������������
(1)Ƶ�ʷֲ�ֱ��ͼ��С���������֮��Ϊ1���ݴ����![]() ��
��
(2)������ɵ�![]() ���ɶ���ֲ��������г��ֲ��У�Ȼ���������������Ϊ
���ɶ���ֲ��������г��ֲ��У�Ȼ���������������Ϊ![]()
(3)���Ƶ�ʷֲ�ֱ��ͼ�����ʽⷽ�̿ɵã� ![]() .
.
���������
�⣺
��1��![]()
![]()
��2��������Ӹó��о����г�ȡ��ˮ��������3�ֵĸ���Ϊ
![]()
��![]()
��![]()
![]()
| 0 | 1 | 2 | 3 |
| 0.729 | 0.243 | 0.027 | 0.001 |
![]()
��3������ˮ������3�ֵľ���ռ10%������![]()
![]() ��Ԫ��.
��Ԫ��.


 �¿α�������������ҵ�������γ�����ϵ�д�
�¿α�������������ҵ�������γ�����ϵ�д� ����ν����Ž̲��㽭���̴�ѧ������ϵ�д�
����ν����Ž̲��㽭���̴�ѧ������ϵ�д� �����Ļ������������������ϵ�д�
�����Ļ������������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �У�
�У� ![]() ƽ��
ƽ��![]() ��
�� ![]() ��
�� ![]() ����
����![]() ��
�� ![]() Ϊ�߶�
Ϊ�߶�![]() ��һ��.
��һ��.
��1����֤��ƽ��![]() ƽ��
ƽ��![]() ��
��
��2����![]() ��
��![]() ����֤��
����֤�� ![]() ƽ��
ƽ��![]() ����������
����������![]() �����.
�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�Ľ�A��B��C���Եı߷ֱ���a��b��c�������� ![]() ��
�� ![]() ��
�� ![]() ��
��
��1���� ![]() ��
�� ![]() ����֤����ABCΪ���������Σ�
����֤����ABCΪ���������Σ�
��2���� ![]() ��
�� ![]() ���߳�c=2����C=
���߳�c=2����C= ![]() �����ABC�������
�����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���ԲC��Բ���ڵ�һ���ޣ�ԲC��x���ཻ��A��1��0����B��3��0�����㣬����ֱ��x��y+1=0���У���ԲC�ı�����Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() ������
������![]() ��ֱ��
��ֱ��![]() ��Բ
��Բ![]() ��
��![]() ���㣬�ֱ��
���㣬�ֱ��![]() ������Բ�����ߣ������������ཻ�ڵ�
������Բ�����ߣ������������ཻ�ڵ�![]() ʱ�����
ʱ�����![]() �Ĺ켣����Ϊ__________��
�Ĺ켣����Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
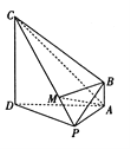
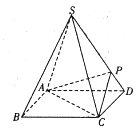
����Ŀ����ͼ������![]() �ĵ����������Σ�ÿ������ij����ǵ���߳���
�ĵ����������Σ�ÿ������ij����ǵ���߳���![]() ����PΪ����SD�ϵĵ㣬��
����PΪ����SD�ϵĵ㣬��![]() .
.
��1��������![]() �Ĵ�С��
�Ĵ�С��
��2���ڲ���SC���Ƿ����һ��E��ʹ��![]() ƽ��
ƽ��![]() �������ڣ���
�������ڣ���![]() ��ֵ���������ڣ���˵������.
��ֵ���������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ�ü��������������ȡ��30��ͬѧ������ÿ��ƽ�������Ķ�ʱ�䣨��λ��Сʱ�����е��飬��Ҷͼ��ͼ��
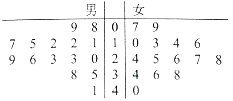
�����¾������Ķ�ʱ�䲻����30Сʱ��ѧ����Ϊ�������ԡ�.
��1����Ƶ����Ϊ���ʣ����Ƹ�У900��ѧ���С������ԡ��ж����ˣ�
��2�����ѳ�ȡ��7���������ԡ��������ȡ�С�Ů�������ԡ���1�ˣ��μӶ����������.
��i�����ж����ֲ�ͬ�ij�ȡ������
��ii�����ȡ���С�Ů��λ�������ԡ��¾�����ʱ��������2Сʱ�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() ��
��![]() ��
�� ![]() ���㣬��Բ��
���㣬��Բ��![]() ��ֱ��
��ֱ��![]() ��.
��.
��1����Բ![]() �ķ��̣�
�ķ��̣�
��2����ֱ��![]() ����
����![]() �ұ�Բ
�ұ�Բ![]() �صõ��߶γ�Ϊ
�صõ��߶γ�Ϊ![]() ����
����![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com