
【题目】某种产品的广告费支出![]() (百万元)与销售额
(百万元)与销售额![]() (百万元)之间有如下对应数据:
(百万元)之间有如下对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 50 | 60 | 70 |
如果![]() 与
与![]() 之间具有线性相关关系.
之间具有线性相关关系.
(1)作出这些数据的散点图;
(2)求这些数据的线性回归方程![]() ;
;
(3)预测当广告费支出为9百万元时的销售额。 ( 参考数据: ![]() )
)
 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
【题目】运货卡车以每小时x千米的速度匀速行驶130千米(50≤x≤100)(单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油(2+ ![]() )升,司机的工资是每小时14元.
)升,司机的工资是每小时14元.
(1)求这次行车总费用y关于x的表达式;
(2)当x为何值时,这次行车的总费用最低,并求出最低费用的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为椭圆
为椭圆![]() 的左右焦点,点
的左右焦点,点![]() 为其上一点,且有
为其上一点,且有![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,过
两点,过![]() 与
与![]() 平行的直线
平行的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 的面积
的面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形, ![]() ,四边形
,四边形![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点.
的中点.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}为等差数列,a1+a3+a5=105,a2+a4+a6=99,以Sn表示{an}的前n项和,则使得Sn达到最大值的n是( )
A.21
B.20
C.19
D.18
查看答案和解析>>
科目:高中数学 来源: 题型:
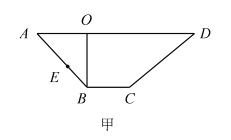
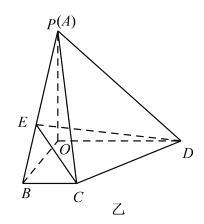
【题目】如图甲所示, ![]() 是梯形
是梯形![]() 的高,
的高, ![]() ,
, ![]() ,
, ![]() ,现将梯形
,现将梯形![]() 沿
沿![]() 折起如图乙所示的四棱锥
折起如图乙所示的四棱锥![]() ,使得
,使得![]() ,点
,点![]() 是线段
是线段![]() 上一动点.
上一动点.
(1)证明: ![]() 和
和![]() 不可能垂直;
不可能垂直;
(2)当![]() 时,求
时,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,l1,l2是通过某城市开发区中心O的两条南北和东西走向的街道,连结M、N两地之间的铁路线是圆心在l2上的一段圆弧.若点M在点O正北方向,且|MO|=3 km,点N到l1,l2的距离分别为4 km和5 km.

(1)建立适当的坐标系,求铁路线所在圆弧的方程;
(2)若该城市的某中学拟在点O正东方向选址建分校,考虑环境问题,要求校址到点O的距离大于4 km,并且铁路线上任意一点到校址的距离不能少于![]() km,求该校址距点O的最近距离.(注:校址视为一个点)
km,求该校址距点O的最近距离.(注:校址视为一个点)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com