
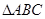 所在平面
所在平面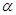 外一点
外一点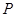 ,作
,作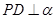 ,垂足为D,若
,垂足为D,若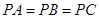 ,则D是
,则D是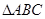 的 心.(从外心,内心,重心,垂心中选一个)
的 心.(从外心,内心,重心,垂心中选一个) 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
 计到达的区域安排了同一条直线上的三个救援中心(记为
计到达的区域安排了同一条直线上的三个救援中心(记为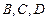 ).当返回舱距地面1万米的
).当返回舱距地面1万米的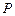 点时(假定以后垂直下落,并在
点时(假定以后垂直下落,并在 点着陆),
点着陆),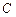 救援中心测得飞船位于其南偏东
救援中心测得飞船位于其南偏东 方向,仰角为
方向,仰角为 ,
,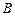 救援中心测得飞船位于其南偏西
救援中心测得飞船位于其南偏西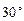 方向,仰角为
方向,仰角为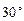 .
.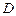 救援中心测得着陆点
救援中心测得着陆点 位于其正东方向.
位于其正东方向.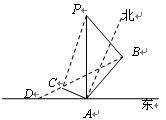
 两救援中心间的距离;
两救援中心间的距离; 救援中心与着陆点
救援中心与着陆点 间的距离.
间的距离.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 中,角
中,角 的对边分别为
的对边分别为 ,下列四个命题
,下列四个命题 ,则
,则 ;②若
;②若 ,则满足条件的三角形共有两个;③若
,则满足条件的三角形共有两个;③若 成等差数列,
成等差数列, 成等比数列,则
成等比数列,则 为正三角形;④若
为正三角形;④若 ,则
,则 .其中正确命题的个数是( )
.其中正确命题的个数是( )| A.1个 | B.2个 | C.3个 | D.4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com