
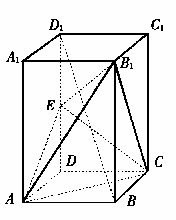
已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EACD1B,且面EAC与底面ABcD所成的角为45°,AB=a
(Ⅰ)求截而EAC的面积:
(Ⅱ)求异面直线A1B1与AC之间的距离;
(Ⅲ)求三棱锥B1-EAC的体积
(1)解:如图,连结DB交AC于O,连结EO。
∵底面ABCD是正方形∴DO⊥AC。
又∵ED⊥底面AC,∴EO⊥AC。
∴∠EOD是面EAC与底面AC所成二面角的平面角,
∴ ∠EOD=45°。
DO=(2)1/2/2a, AC=(2)1/2a, Eo=[(2)1/2a?sec45°]/2=a.
故 S△EAC=(2)1/2×a2/2 4分
(II)解:由题设ABCD-A1B1C1D1是正四棱柱,得A1A⊥底面AC, A1A⊥AC。
又 A1A⊥A1B1,∴A1A是异面直线A1B1与AC间的公垂线。
∵D1B∥面EAC,且面D1BD与面EAC交线为EO,∴ D1B∥EO。
又 O是DB的中点,∴E是D1D的中点, D1B=2ED=2a。
异面直线A1B1与AC间的距离为(2)1/2a。
(III)解法一:如图,连结D1B1。
∵D1D=DB=(2)1/2a,∴BDD1B1是正方形。
连结B1D交D1B于P,交EO于Q。
∵B1D⊥D1B。 EO∥D1B,∴B1D⊥EO
又 AC⊥EO, AC⊥ED,∴AC⊥面BDD1B1∴B1D⊥AC∴B1D⊥面EAC。
∴B1Q是三棱锥B1-EAC的高。
由DQ=PQ,得B1Q=3B1D/4=3a/2。
∴VB1-EAC=(1/3)?[(2)1/2a2/2]?(3/20=(2)1/2?a3/4.
所以三棱锥了-EAC的体积是(2)1/2?a3/4.
解法二:连结B1O,则VB1-EAC=2VA-EOB1。
∵AO⊥面BDD1B1,∴AO是三棱锥A-EOB1的高,AO=(2)1/2?a/2
在正方形BDD1B1中,E、O分别是D1D、DB的中点(如右图),
则S△EOB1=3a2/4.∴VB1-EAC=2×(1/30×(3a2/4)×[(2)1/2a/2}=(2)1/2?a3/4.
所以三棱锥B1-EAC的体积是(2)1/2?a3/4.。



 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
 如图所示,已知正四棱柱ABCD-A1B1C1D1的底面边长为1,点E在棱AA1上,A1C∥平面EBD,截面EBD的面积为
如图所示,已知正四棱柱ABCD-A1B1C1D1的底面边长为1,点E在棱AA1上,A1C∥平面EBD,截面EBD的面积为
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知正四棱柱ABCD-A1B1C1D1与它的侧视图(或称左视图),E是DD1上一点,AE⊥B1C.
如图,已知正四棱柱ABCD-A1B1C1D1与它的侧视图(或称左视图),E是DD1上一点,AE⊥B1C.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2006•广州模拟)已知正四棱柱ABCD-A1B1C1D1,AB=BC=1,AA1=2,点E为CC1的中点,点F为BD1的中点.
(2006•广州模拟)已知正四棱柱ABCD-A1B1C1D1,AB=BC=1,AA1=2,点E为CC1的中点,点F为BD1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com