练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知等式：sin25°+cos235°+sin5°cos35°= ； sin215°+cos245°+sin15°cos45°= ； sin230°+cos260°+sin30°cos60°= ；由此可归纳出对任意角度θ都成立的一个等式，并予以证明．

    【答案】解：根据各式的共同特点可得：等式左边余弦均为正弦度数加30°，右边是常数 ，

    则具有一般规律的等式：sin2θ+cos2（θ+30°）+sinθcos（θ+30°）= ，

    证明：等式的左边=sin2θ+cos（θ+30°）[cos（θ+30°）+sinθ]

    =sin2θ+（ cosθ﹣ sinθ）（ +sinθ）

    =sin2θ+（ ）

    = = =右边，

    ∴等式成立．


    【解析】根据所给的等式归纳：等式左边余弦均为正弦度数加30°，右边是常数，按照此规律写出一般性的结论，利用两角和的余弦公式等进行证明等式成立．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知在（ ﹣ ）n的展开式中，第6项为常数项．
    （1）求n；
    （2）求含x2项的系数；
    （3）求展开式中所有的有理项．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数的图象与轴交于点，周期是．

    （1）求函数解析式，并写出函数图象的对称轴方程和对称中心；

    （2）已知点，点是该函数图象上一点，点是的中点，当 ， 时，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某电子商务公司对10 000名网络购物者2017年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.

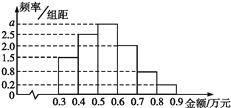
    (1)直方图中的a=_____;

    (2)在这些购物者中,消费金额在区间[0.5,0.9]内的购物者的人数为_______.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，．

    （1）判断函数的奇偶性，并证明．

    （2）若，，求的值．

    （3）若不等式在上恒成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设X是一个离散型随机变量，则下列不能成为X的概率分布列的一组数据是（ ）
    A.0， ，0，0，
    B.0.1，0.2，0.3，0.4
    C.p，1﹣p（0≤p≤1）
    D. ， ，…，

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若函数在区间上存在零点，求实数的取值范围；

    （2）当时，若对任意的，总存在，使成立，求实数的取值范围；

    （3）若的值域为区间，是否存在常数，使区间的长度为？若存在，求出的值；若不存在，请说明理由.（注：区间的长度为）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xOy中，曲线C的参数方程为 （θ为参数）．以坐标原点为极点，以x轴的正半轴为极轴，建立极坐标系．
    （1）写出曲线C的极坐标方程；
    （2）设点M的极坐标为（ ），过点M的直线l与曲线C相交于A，B两点，若|MA|=2|MB|，求AB的弦长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】电脑游戏中,“主角”的生存机会往往被预先设定,如某枪战游戏中,“主角”被设定生存机会5次,每次生存承受射击8枪(被击中8枪则失去一次生命机会).假设射击过程均为单子弹发射,试为“主角”耗用生存机会的过程设计一个算法,并画出程序框图.

    查看答案和解析>>

    同步练习册答案