选修4-5:不等式选讲
若关于x的方程 x2-4x+|a|+|a-3|=0有实根
(1)求实数a的取值集合A
(2)若存在a∈A,使得不等式t2-2a|t|+12<0成立,求实数t的取值范围.
解:(1)∵关于x的方程 x
2-4x+|a|+|a-3|=0有实根,
∴△=16-4(|a|+|a-3|)≥0,
即
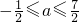
,
∴A=[
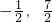
];
(2)令f(a)=t
2-2a|t|+12,
∵存在a∈A,使得不等式t
2-2a|t|+12<0成立,
∴f(a)
min<0即可,即f(

)=t
2-7|t|+12<0,
∴3<|t|<4,
∴-4<t<-3或3<t<4.
分析:(1)根据关于x的方程 x
2-4x+|a|+|a-3|=0有实根,可得△≥0,解不等式即可求得结果;
(2)存在a∈A,使得不等式t
2-2a|t|+12<0成立,构造函数f(a)=t
2-2a|t|+12,转化为函数的最小值小于零即可,解此不等式即可求得实数t的取值范围.
点评:本题考查二次函数的根的问题,别更主元,构造函数f(a)=t
2-2a|t|+12,转化为函数的最小值是解题的关键和难点,考查运算能力和转化能力,属中档题.

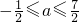 ,
,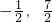 ];
]; )=t2-7|t|+12<0,
)=t2-7|t|+12<0,
