
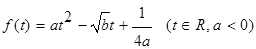 的最大值为正实数,集合
的最大值为正实数,集合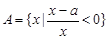 ,集合
,集合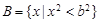 。
。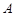 和
和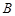 ;
;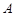 与
与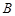 的差集:
的差集: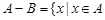 且
且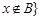 。
。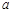 ,
,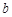 ,
,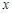 均为整数,且
均为整数,且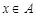 。
。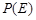 为
为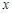 取自
取自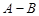 的概率,
的概率,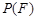 为
为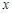 取自
取自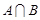 的概率,写出
的概率,写出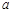 与
与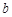 的二组值,使
的二组值,使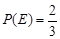 ,
,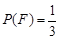 。
。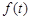 中,
中,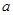 ,
,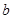 是(2)中
是(2)中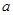 较大的一组,试写出
较大的一组,试写出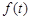 在区间[
在区间[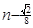 ,n]上的最 大值函数
,n]上的最 大值函数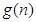 的表达式。
的表达式。  天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
 是函数
是函数 的一个极值,称点
的一个极值,称点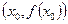 是函数
是函数 的一个极值点.已知函数
的一个极值点.已知函数
 总存在有两个极值点
总存在有两个极值点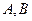 ,求
,求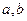 所满足的关系;
所满足的关系; 有两个极值点
有两个极值点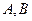 ,且存在
,且存在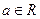 ,求
,求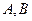 在不等式
在不等式 表示的区域内时实数
表示的区域内时实数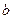 的范围.
的范围. 恰有一个极值点
恰有一个极值点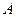 ,且存在
,且存在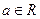 ,使
,使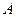 在不等式
在不等式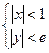 表示的区域内,证明:
表示的区域内,证明: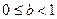 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
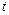 元(其中
元(其中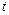 为常数,且
为常数,且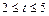 ),设该工厂每件玩具的出厂价为
),设该工厂每件玩具的出厂价为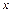 元(
元(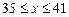 ),根据市场调查,日销售量与
),根据市场调查,日销售量与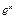 (
(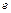 为自然对数的底数)成反比例,当每件玩具的出厂价为40元时,日销售量为10件.
为自然对数的底数)成反比例,当每件玩具的出厂价为40元时,日销售量为10件.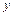 (元)与每件玩具的出厂价
(元)与每件玩具的出厂价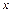 元的函数关系式;
元的函数关系式;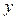 最大,并求
最大,并求 的最大值.
的最大值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
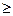 g(x)恒成立,求实数c的取值范围;
g(x)恒成立,求实数c的取值范围;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
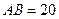 km,
km, 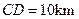 ,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且A,B与等距离的一点O处建造一个污水处理厂,并铺设排污管道AO,BO,OP,设排污管道的总长为ykm。
,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且A,B与等距离的一点O处建造一个污水处理厂,并铺设排污管道AO,BO,OP,设排污管道的总长为ykm。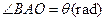 ,将
,将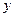 表示成
表示成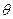 的函数关系式;
的函数关系式;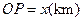 ,将
,将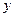 表示成
表示成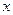 的函数关系式。
的函数关系式。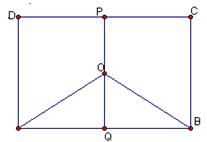
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 艘产值函数为
艘产值函数为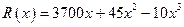 (单位:万元),成本函数
(单位:万元),成本函数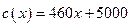 (单位:万元),又在经济学中,函数
(单位:万元),又在经济学中,函数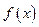 的边际函数
的边际函数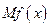 定义为
定义为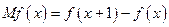
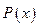 及边际利润函数
及边际利润函数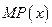 (利润=产值—成本)
(利润=产值—成本)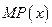
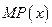 的单调递减区间
的单调递减区间查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 上规划出一块长方形地面建造公园,公园一边落在CD上,但不得越过文物保护区
上规划出一块长方形地面建造公园,公园一边落在CD上,但不得越过文物保护区 的EF.问如何设计才能使公园占地面积最大,并求这最大面积.( 其中AB=200m,BC=160m,AE=60m,AF=40m.)
的EF.问如何设计才能使公园占地面积最大,并求这最大面积.( 其中AB=200m,BC=160m,AE=60m,AF=40m.)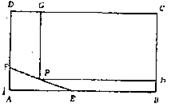
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com