练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．抛物线y2=4x与直线y=-2x+4所围成的面积为$\frac{86}{3}$．

    分析 求出抛物线和直线的交点，选y作积分变量，利用定积分求面积即可．

    解答 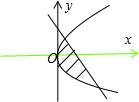解：由曲线y2=4x与直线y=-2x+4，解出抛物线和直线的交点为（1，2）及（4，-4）．
    选y作积分变量，将曲线方程写为x=$\frac{{y}^{2}}{4}$及x=2-$\frac{1}{2}$y．
    S=${∫}_{-4}^{2}$[（2-$\frac{1}{2}$y）-$\frac{{y}^{2}}{4}$]dy=（2y-y2-$\frac{{y}^{3}}{12}$）${|}_{-4}^{2}$=$\frac{86}{3}$．
    故答案为：$\frac{86}{3}$．

    点评 本题考查利用定积分求面积，考查学生的计算能力，比较基础．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    11．方程log3x+x-3=0的解所在区间是（k，k+1）（k∈Z），则k=2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．函数$y=sin（-\frac{x}{2}-\frac{π}{6}）$的单调递增区间是（　　）
    A．[2kπ+$\frac{2}{3}$π，2kπ+$\frac{8}{3}$π]（k∈Z）B．[4kπ+$\frac{2}{3}$π，4kπ+$\frac{8}{3}$π]（k∈Z）
    C．[2kπ-$\frac{4}{3}$π，2kπ+$\frac{2}{3}$π]（k∈Z）D．[4kπ-$\frac{4}{3}$π，4kπ+$\frac{2}{3}$π]（k∈Z）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．原命题：“设复数z=a+bi（i为虚数单位），若z为纯虚数，则a=0”的逆命题、否命题、逆否命题中真命题共有1个．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．某制造商制造并出售球形瓶装的某种饮料．瓶子的制造成本是0.8πr2分，其中r是瓶子的半径，单位是cm．已知每出售1ml的饮料，制造商可获利0.2分，且制造商能制做的瓶子的最大半径为6cm．
    问题：瓶子半径多大时，能使每瓶饮料的利润最大？瓶子半径多大时，每瓶饮料的利润最小？$（{V_球}=\frac{4}{3}π{r^3}）$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．点P在曲线C：$\frac{x^2}{4}+{y^2}$=1上，若存在过点P的直线交曲线C于A点，交直线l：x=4于B点，且满足|PA|=|PB|，则称P点为“二中点”，那么下列结论正确的是（　　）
    A．曲线C上的所有点都是“二中点”
    B．曲线C上的仅有有限个点是“二中点”
    C．曲线C上的所有点都不是“二中点”
    D．曲线C上的有无穷多个点（但不是所有的点）是“二中点”

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．求顶点在X轴，且两顶点的距离是8，$e=\frac{5}{4}$的双曲线标准方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知函数$f（x）={log_a}\frac{x-2}{x+2}$（a＞0且a≠1）
    （1）求f（x）的定义域并判定f（x）的奇偶性；
    （2）当a＞1时，判定f（x）的单调性并用定义法证明；
    （3）是否存在实数a，使得f（x）的定义域为[m，n]时，值域为[1+logan，1+logam]？若存在，求出实数a的取值范围；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知函数f（x）满足f（x-1）=x2，则f（x）的解析式为（　　）
    A．f（x）=（x+1）2B．f（x）=（x-1）2C．f（x）=x2+1D．f（x）=x2-1

    查看答案和解析>>

    同步练习册答案