如图，在五面体ABCDEF中，四边形ABCD是矩形，DE⊥平面ABCD．
（1）求证：AB∥EF；
（2）求证：平面BCF⊥平面CDEF．
（1）详见解析，（2）详见解析.
解析试题分析：（1）证明线线平行，一般思路为利用线面平行的性质定理与判定定理进行转化. 因为四边形ABCD是矩形，所以AB∥CD，因为
平面CDEF，
平面CDEF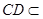，所以AB∥平面CDEF．因为
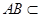平面ABFE，平面
平面
，所以AB∥EF．（2）证明面面垂直，一般利用其判定定理证明，即先证线面垂直. 因为DE⊥平面ABCD，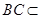
平面ABCD，所以DE⊥BC．因为BC⊥CD，
，
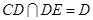平面CDEF，所以BC⊥平面CDEF．因为BC
平面BCF，平面BCF⊥平面CDEF．
【证】（1）因为四边形ABCD是矩形，所以AB∥CD，
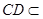因为平面CDEF，平面CDEF，
所以AB∥平面CDEF． 4分
因为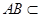平面ABFE，平面平面，
所以AB∥EF． 7分
（2）因为DE⊥平面ABCD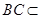，平面ABCD，
所以DE⊥BC． 9分
因为BC⊥CD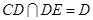，，平面CDEF，
所以BC⊥平面CDEF． 12分
因为BC平面BCF，平面BCF⊥平面CDEF． 14分
考点：线面平行与垂直关系
备战中考寒假系列答案科目：高中数学 来源： 题型：解答题
如图，在四棱锥P—ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC＝90°，平面PAD⊥底面ABCD，Q为AD的中点，M是棱PC上的点，PA＝PD＝2，BC＝
AD＝1，CD＝
.
(1)若点M是棱PC的中点，求证：PA∥平面BMQ；
(2)若二面角M—BQ—C为30°，设PM＝tMC，试确定t的值．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
定理：如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线就和两平面的交线平行．
请对上面定理加以证明，并说出定理的名称及作用．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知四棱锥P-ABCD中，PB⊥平面ABCD，底面ABCD是直角梯形,∠ABC=∠BCD=90°，PB=BC=CD=
AB.Q是PC上的一点.
⑴求证：平面PAD⊥面PBD;
⑵当Q在什么位置时，PA∥平面QBD?
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
如图，在直三棱柱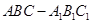
中，D、E分别是BC和
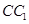的中点，已知AB=AC=AA1=4，ÐBAC=90°.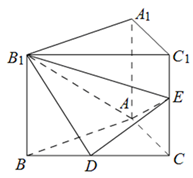
（1）求证：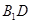
⊥平面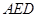
；
（2）求二面角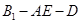
的余弦值；
（3）求三棱锥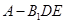
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
中，底面
为平行四边形，
底面
平面
;
大小为
，求
与平面
所成角的正弦值.
中，底面
是正方形，
，
，点
在
上，且
.
平面
的余弦值；
上存在点
，使
∥平面
，并求
的长.
为正方形，四边形
是直角梯形，
，
平面
．
平面
；
与平面
中，四边形
是边长为
的正方形，
平面
，
，
，
.
平面
；
与平面
所成角的正切值.