
【题目】已知![]() 是定义在
是定义在![]() 上的函数,记
上的函数,记![]() ,
,![]() 的最大值为
的最大值为![]() .若存在
.若存在![]() ,满足
,满足![]() ,
,![]() ,
,![]() ,则称一次函数
,则称一次函数![]() 是
是![]() 的“逼近函数”此时的
的“逼近函数”此时的![]() 称为
称为![]() 在
在![]() 上的“逼近确界”.
上的“逼近确界”.
(1)验证![]() 是
是![]() ,
,![]() 的“逼近函数”;
的“逼近函数”;
(2)已知![]() ,
,![]() ,
,![]() .若
.若![]() 是
是![]() 的“逼近函数”,求a,b的值;
的“逼近函数”,求a,b的值;
(3)已知![]() ,
,![]() ,求证;对任意常数a,b,
,求证;对任意常数a,b,![]() .
.
【答案】(1)见解析;(2)a![]() .b
.b![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)记G(x)=2x2﹣(4x﹣1)=2(x﹣1)2﹣1,x∈[0,2].利用二次函数的单调性可得|G(x)|的最大值为1,且G(0)=1,G(1)=﹣1,G(2)=1.
(2)F(x)![]() (ax+b),由
(ax+b),由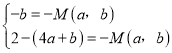 ,可得M(a,b)=b,a
,可得M(a,b)=b,a![]() .存在x0∈(0,4)满足F(x2)=M(a,b),即F(a,b)max=F(x2)=b,即可得出.
.存在x0∈(0,4)满足F(x2)=M(a,b),即F(a,b)max=F(x2)=b,即可得出.
(3)M(a,b)![]() |t﹣at2﹣b|
|t﹣at2﹣b|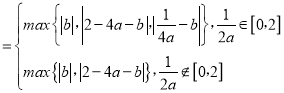 .即可得出.
.即可得出.
(1)记G(x)=2x2﹣(4x﹣1)=2(x﹣1)2﹣1,x∈[0,2].则|G(x)|的最大值为1,
且G(0)=1,G(1)=﹣1,G(2)=1.故y=4x﹣1是g(x)=2x2,x∈[0,2]的“逼近函数”.
(2)F(x)![]() (ax+b),由
(ax+b),由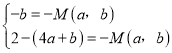 ,可得M(a,b)=b,a
,可得M(a,b)=b,a![]() .
.
存在x0∈(0,4)满足F(x2)=M(a,b),即F(a,b)max=F(x2)=b,
即F(x)![]() x﹣b
x﹣b![]() b,故x2=1.
b,故x2=1.
由F(1)![]() b=b,可得b
b=b,可得b![]() .
.
(3)证明:M(a,b)![]() |t﹣at2﹣b
|t﹣at2﹣b
|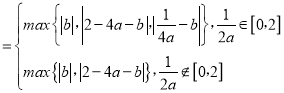 .
.
当![]() [0,2]时,2M(a,b)≥|b|+|2﹣4a﹣b|≥|2﹣4a|>1,故M(a,b)
[0,2]时,2M(a,b)≥|b|+|2﹣4a﹣b|≥|2﹣4a|>1,故M(a,b)![]() .
.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:
【题目】某医院为筛查某种疾病,需要检验血液是否为阳性,现有![]() 份血液样本,有以下两种检验方式:①逐份检验,列需要检验
份血液样本,有以下两种检验方式:①逐份检验,列需要检验![]() 次;②混合检验,将其
次;②混合检验,将其![]() (
(![]() 且
且![]() )份血液样本分别取样混合在一起检验.若检验结果为阴性,这
)份血液样本分别取样混合在一起检验.若检验结果为阴性,这![]() 份的血液全为阴性,因而这
份的血液全为阴性,因而这![]() 份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这
份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这![]() 份血液究竟哪几份为阳性,就要对这
份血液究竟哪几份为阳性,就要对这![]() 份再逐份检验,此时这
份再逐份检验,此时这![]() 份血液的检验次数总共为
份血液的检验次数总共为![]() 次.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为
次.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为![]() .
.
(1)假设有5份血液样本,其中只有2份样本为阳性,若采用逐份检验的方式,求恰好经过3次检验就能把阳性样本全部检验出来的概率.
(2)现取其中![]() (
(![]() 且
且![]() )份血液样本,记采用逐份检验方式,样本需要检验的总次数为
)份血液样本,记采用逐份检验方式,样本需要检验的总次数为![]() ,采用混合检验方式,样本需要检验的总次数为
,采用混合检验方式,样本需要检验的总次数为![]() .
.
(i)运用概率统计的知识,若![]() ,试求
,试求![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ;
;
(ii)若![]() ,且采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求
,且采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求![]() 的最大值.
的最大值.
参考数据:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】江心洲有一块如图所示的江边,![]() ,
,![]() 为岸边,岸边形成
为岸边,岸边形成![]() 角,现拟在此江边用围网建一个江水养殖场,有两个方案:方案l:在岸边
角,现拟在此江边用围网建一个江水养殖场,有两个方案:方案l:在岸边![]() 上取两点
上取两点![]() ,用长度为
,用长度为![]() 的围网依托岸边线
的围网依托岸边线![]() 围成三角形
围成三角形![]() (
(![]() ,
,![]() 两边为围网);方案2:在岸边
两边为围网);方案2:在岸边![]() ,
,![]() 上分别取点
上分别取点![]() ,用长度为
,用长度为![]() 的围网
的围网![]() 依托岸边围成三角形
依托岸边围成三角形![]() .请分别计算
.请分别计算![]() ,
,![]() 面积的最大值,并比较哪个方案好.
面积的最大值,并比较哪个方案好.
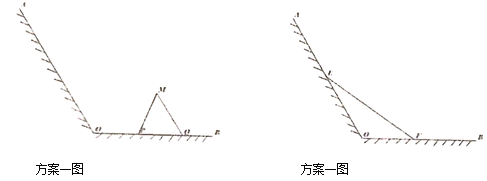
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在![]() 轴上,左顶点为
轴上,左顶点为![]() ,左焦点为
,左焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,直线
上,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,直线
两点,直线![]() ,
, ![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
, ![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)以![]() 为直径的圆是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
为直径的圆是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着自媒体直播平台的迅猛发展,直播平台上涌现了许多知名三农领域创作者,通过直播或视频播放,帮助当地农民在直播平台上销售了大量的农产品,促进了农村的经济发展,当地农业与农村管理部门对近几年的某农产品年产量进行了调查,形成统计表如下:
年份 |
|
|
|
|
|
|
年份代码 |
|
|
|
|
|
|
年产量 |
|
|
|
|
|
|
(1)根据表中数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据线性回归方程预测![]() 年该地区该农产品的年产量;
年该地区该农产品的年产量;
(3)从![]() 年到
年到![]() 年的
年的![]() 年年产量中随机选出
年年产量中随机选出![]() 年的产量进行具体调查,求选出的
年的产量进行具体调查,求选出的![]() 年中恰有一年的产量小于
年中恰有一年的产量小于![]() 万吨的概率.
万吨的概率.
附:对于一组数据![]() 、
、![]() 、
、![]() 、
、![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
,![]() .(参考数据:
.(参考数据:![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com