【题目】在各项均为正数的等比数列 
中， 
，且 
成等差数列.
（1）求等比数列 的通项公式；
（2）若数列 
满足 
，求数列 的前 
项和 
的最大值.
【答案】
（1）解：设数列{an}的公比为q ， an＞0
因为2a1 ， a3 ， 3a2成等差数列，
所以2a1+3a2=2a3 ，
即 
，
所以2q2-3q-2=0，
解得q=2或 
（舍去），
又a1=2，所以数列{an}的通项公式
（2）解：由题意得，bn=11-2log2an=11-2n ，
则b1=9，且bn+1-bn=-2，
故数列{bn}是首项为9，公差为-2的等差数列，
所以 
=-（n-5）2+25，
所以当n=5时，Tn的最大值为25
【解析】（1）将2a1 ， a3 ， 3a2以a和q的形式表示，再利用成等差，解得q的值，即得an的通项公式。
（2）将an的通项公式代入bn中，求出bn的首项和公差，再用前n项和公式即可求出。
【考点精析】认真审题，首先需要了解等差数列的前n项和公式(前n项和公式：
)，还要掌握等比数列的通项公式（及其变式）(通项公式：
)的相关知识才是答题的关键．
科目：高中数学 来源： 题型：
【题目】设x，y满足约束条件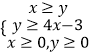 
，若目标函数2z=2x+ny（n＞0），z的最大值为2，则y=tan（nx+ 
）的图象向右平移 后的表达式为（ ）
A.y=tan（2x+ ）
B.y=tan（x﹣ ）
C.y=tan（2x﹣ ）
D.y=tan2x
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了解学生身高情况，某校以10%的比例对全校700名学生按性别进行抽样检查，测得身高情况的统计图如图所示：
(1)估计该校男生的人数；
(2)估计该校学生身高在170～185cm的概率；
(3)从样本中身高在180～190cm的男生中任选2人，求至少有1人身高在185～190cm的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】(1)等差数列{an}中，a1＋3a8＋a15＝120，求2a9－a10的值；
(2)在等差数列{an}中，a15＝8，a60＝20，求a75的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知连续不断函数
，
，
，
（1）证明：函数
在区间
上有且只有一个零点；
（2）现已知函数
在上单调递增，且都只有一个零点（不必证明），记三个函数
的零点分别为
。
求证：Ⅰ)
；
Ⅱ）判断
与
的大小，并证明你的结论。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】若圆(x－1)2＋(y＋1)2＝R2上有且仅有两个点到直线4x＋3y＝11的距离等于1，则半径R的取值范围是( )
A. R＞1 B. R＜3 C. 1＜R＜3 D. R≠2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
