
【题目】已知函数![]() ,
,![]() .(
.(![]() 为自然对数的底数)
为自然对数的底数)
(1)设![]() ;
;
①若函数![]() 在
在![]() 处的切线过点
处的切线过点![]() ,求
,求![]() 的值;
的值;
②当![]() 时,若函数
时,若函数![]() 在
在![]() 上没有零点,求
上没有零点,求![]() 的取值范围.
的取值范围.
(2)设函数![]() ,且
,且![]() ,求证:当
,求证:当![]() 时,
时,![]() .
.
【答案】(1) ![]() ,
,![]() (2)见解析
(2)见解析
【解析】试题分析:(1)①由![]() 和
和![]() 可得在
可得在![]() 处的切线方程,代入点
处的切线方程,代入点![]() 得
得![]() ;
;
②当![]() ,可得
,可得![]() ,讨论
,讨论![]() 和
和![]() 时函数的单调性进而研究零点即可;
时函数的单调性进而研究零点即可;
(2)![]() 等价于
等价于![]() ,令
,令![]() ,求得求最值即可证得.
,求得求最值即可证得.
试题解析:
(1)①由题意,得![]() ,
,
所以函数![]() 在
在![]() 处的切线斜率
处的切线斜率![]() ,又
,又![]() ,
,
所以函数![]() 在
在![]() 处的切线方程
处的切线方程![]() ,
,
将点![]() 代入,得
代入,得![]() .
.
②当![]() ,可得
,可得![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调递增,而
上单调递增,而![]() ,
,
所以只需![]() ,解得
,解得![]() ,从而
,从而![]() .
.
当![]() 时,由
时,由![]() ,解得
,解得![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,
,
![]() 单调递增.所以函数
单调递增.所以函数![]() 在
在![]() 上有最小值为
上有最小值为![]() ,
,
令![]() ,解得
,解得![]() ,所以
,所以![]() . 综上所述,
. 综上所述,![]() .
.
(2)由题意,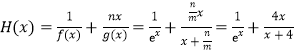 ,
,
而![]() 等价于
等价于![]() .
.
令![]() ,
,
则![]() ,且
,且![]() ,
,![]() .
.
令![]() ,则
,则![]() .
.
因为![]() , 所以
, 所以![]() ,所以导数
,所以导数![]() 在
在![]() 上单调递增,
上单调递增,
于是![]() .
.
从而函数![]() 在
在![]() 上单调递增,即
上单调递增,即![]() .
.
即当![]() 时,
时,![]() .
.


科目:高中数学 来源: 题型:
【题目】椭圆M:![]() 长轴上的两个顶点为
长轴上的两个顶点为![]() 、
、![]() ,点P为椭圆M上除
,点P为椭圆M上除![]() 、
、![]() 外的一个动点,若
外的一个动点,若![]() 且
且![]() ,则动点Q在下列哪种曲线上运动( )
,则动点Q在下列哪种曲线上运动( )
A. 圆 B. 椭圆 C. 双曲线 D. 抛物线
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系.已知直线
轴正半轴为极轴建立极坐标系.已知直线![]() 的参数方程是
的参数方程是 (
(![]() 是参数),圆
是参数),圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆心![]() 的直角坐标;
的直角坐标;
(2)由直线![]() 上的点向圆
上的点向圆![]() 引切线,并切线长的最小值.
引切线,并切线长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的下顶点为
的下顶点为![]() ,右顶点为
,右顶点为![]() ,离心率
,离心率![]() ,抛物线
,抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 是抛物线
是抛物线![]() 上一点,抛物线
上一点,抛物线![]() 在点
在点![]() 处的切线为
处的切线为![]() ,且
,且![]() .
.
(1)求直线![]() 的方程;
的方程;
(2)若![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]() ,求
,求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交管部门为宣传新交规举办交通知识问答活动,随机对该市![]() 岁的人群抽样了
岁的人群抽样了![]() 人,回答问题统计结果如图表所示:
人,回答问题统计结果如图表所示:
分组 | 回答正确的人数 | 回答正确的人数占本组的频率 | |
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
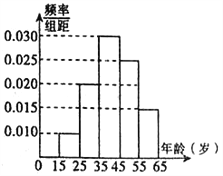
(1)分别求出![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)从第![]() ,
,![]() ,
,![]() 组回答正确的人中用分层抽样方法抽取
组回答正确的人中用分层抽样方法抽取![]() 人,则第
人,则第![]() ,
,![]() ,
,![]() 组每组应各抽取多少人?
组每组应各抽取多少人?
(3)在(2)的前提下,决定在所抽取的![]() 人中随机抽取
人中随机抽取![]() 人颁发幸运奖,求:所抽取的
人颁发幸运奖,求:所抽取的![]() 人中至少有一个第
人中至少有一个第![]() 组的人的概率.
组的人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,墙上有一壁画,最高点![]() 离地面4米,最低点
离地面4米,最低点![]() 离地面2米,观察者从距离墙
离地面2米,观察者从距离墙![]() 米,离地面高
米,离地面高![]() 米的
米的![]() 处观赏该壁画,设观赏视角
处观赏该壁画,设观赏视角![]()
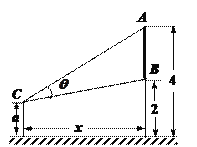
(1)若![]() 问:观察者离墙多远时,视角
问:观察者离墙多远时,视角![]() 最大?
最大?
(2)若![]() 当
当![]() 变化时,求
变化时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() ,(t为参数),在以原点O为极点,
,(t为参数),在以原点O为极点,![]() 轴的非负半轴为极轴建立的极坐标系中,直线
轴的非负半轴为极轴建立的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]() 两点的极坐标分别为.
两点的极坐标分别为.![]()
(1)求圆![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)点![]() 是圆
是圆![]() 上任一点,求
上任一点,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com